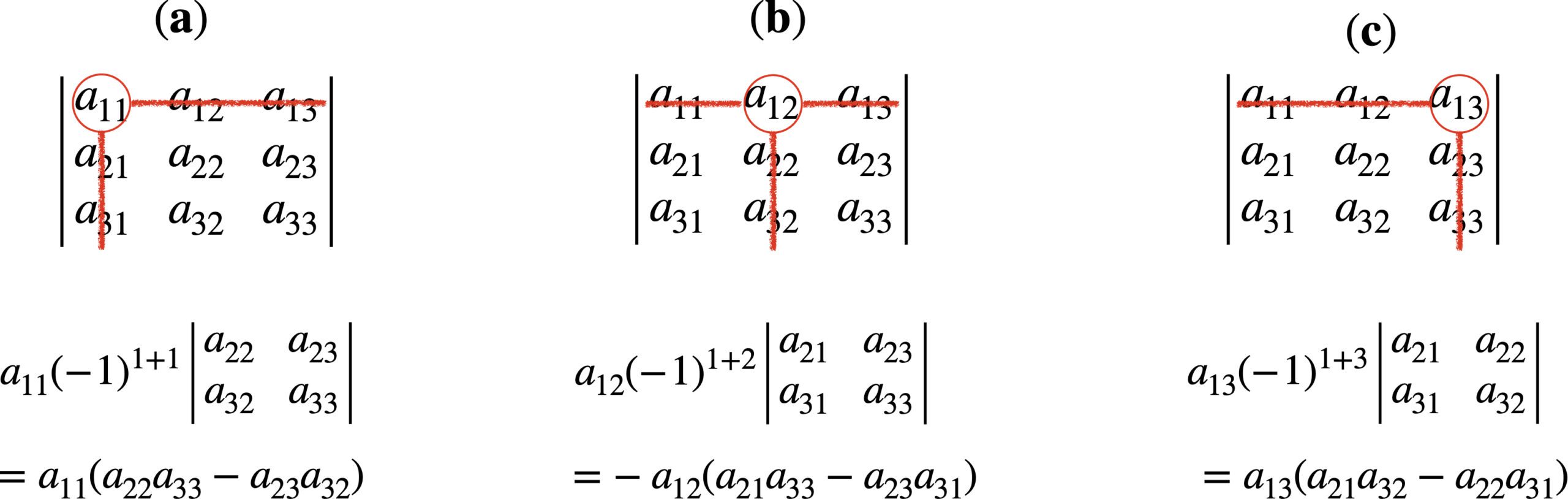여인수 전개(cofactor expansion)5 (1)
행렬식을 여인수 전개로 표현하는 방법을 알아봐요. 여인수 전개(cofactor expansion)란 행렬식(determinant)을 여인수로 전개하여 표현한 것을 말해요. 여인수 전개는 라플라스 전개(Laplace expansion)라고도 불립니다. 이때 여인수(cofactor)의 뜻이 궁금할 텐데요. ‘나머지에서 도출된 수’라는 뜻의 한자어로 행렬 일부를 제외한 나머지 부분에서 도출된 숫자 임을 의미합니다. ‘어른 여자’를 뜻하는 ‘여인’과는 무관해요. 결론부터 말씀드리면 3×3 행렬의 행렬식을 여인수 전개하면 다음과 같아요. 여인수 … Read more