DensityPlot3D : Mathematica

Last Updated on 2024-05-13 by BallPen

매스매티카의 DensityPlot3D와 관련된 몇가지 명령어들을 알아봐요.

DensityPlot3D 명령어는 매스매티카에서 스칼라함수의 그래픽을 그리는데 유용하게 사용될 수 있습니다.

이번 글에서는 DensityPlot3D 뿐만 아니라 SliceDensityPlot3D, Grad, VectorPlot3D, SliceVectorPlot3D 명령어들에 대한 쓰임을 알아보겠습니다.

아래는 이번 글의 목차에요.

Contents

3차원 스칼라함수를 다음과 같이 정의해보겠습니다.

\tag{1} f(x,y,z) = x^2 + y^2 + z^2

이 함수는 원점 (0,0,0)에서의 함수값이 0이 되고, 원점에서 멀어질수록 함수값이 커지게 될 것을 짐작할 수 있어요.

그럼 매스매티카를 이용해 (1)식의 함수를 3차원 그래픽으로 그려봐요. 이때 DensityPlot3D 명령어를 사용하면 됩니다.

코드는 다음과 같아요.

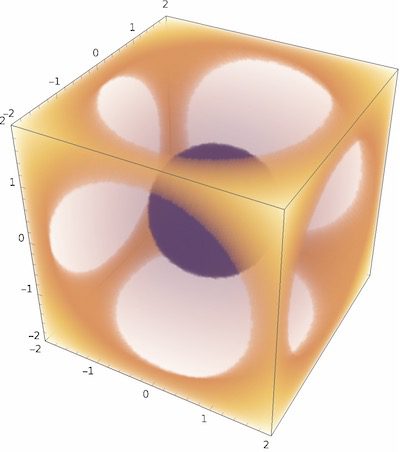
DensityPlot3D[{x^2 + y^2+z^2},{x, -2, 2},{y, -2, 2},{z,-2,2}]

그 결과 [그림 1]을 보면 6면체의 중심에 어떤 구가 있는 것처럼 그려져 있는데요. 보다 정확히 이해하기 위해 SliceDensityPlot3D 명령어를 사용해 볼게요.

SliceDensityPlot3D는 DensityPlot3D의 입체그림을 보고 이해하기 어려울 때 입체의 한 단면을 볼 수 있는 기능이에요.

아래의 코드를 사용해볼께요. [그림 1]에서 $x=-2$ , $x=0$ , $x=2$ 평면에서의 DensityPlot을 보여줍니다.

SliceDensityPlot3D[{x^2 + y^2+z^2},{x==-2, x==0, x==2},{x, -2, 2},{y, -2, 2},{z,-2,2}]

우리가 예상한대로 $x=0$ 평면에서 (0,0,0)의 중심이 가장 어둡게 표현되어 있고 그곳으로부터 멀어질수록 점점 밝아져 함수값이 커지고 있음을 명확히 알 수 있어요.

그렇다면 [그림 2]에 보여진 함수값 변화의 크기와 방향을 전체적으로 알고 싶다면 어떻게 하면 될까요? 이때 기울기(gradient) 연산을 사용하면 좋습니다.

(1)식에 주어진 함수의 기울기 연산 $\nabla f$ 을 위해서는 Grad 명령어를 사용하면 됩니다. 코드는 다음과 같아요.

Grad[{x^2 + y^2+z^2}, {x,y,z}]

그러면 매스매티카가 계산 결과를 다음과 같이 출력해 줄거에요.

{{2 x,2 y,2 z}}

위 출력결과를 우리가 익숙한 형태로 다시 쓰면 다음 식이 됩니다.

\tag{2} \nabla T = 2x \hat x + 2y \hat y + z \hat z

그럼 (2)식을 그래프로 그리면 어떤 모습을 갖는지 궁금할거에요. 이때 사용하는 명령어가 VectorPlot3D 입니다.

다음 코드를 이용하면 3차원 그래픽을 얻을 수 있어요.

VectorPlot3D[{{2 x,2 y,2 z}},{x, -2, 2},{y, -2, 2},{z,-2,2}, VectorScaling -> Automatic, VectorSizes -> Automatic]

중심으로부터 바깥쪽을 향해 함수값이 커지고 있음을 벡터 화살표로 명확히 볼 수 있어요.

그런데 수많은 벡터 화살표들이 있다보니 보기가 불편할 수도 있을거에요. 그러면 이 경우에도 특정한 평면에서의 VectorPlot을 보면 됩니다.

이때 사용하는 명령어가 SliceVectorPlot3D 입니다.

$y=0$ 평면에 대한 VectorPlot을 보려면 다음 코드를 사용하면 됩니다.

SliceVectorPlot3D[{{2 x,2 y,2 z}},{y==0},{x, -2, 2},{y, -2, 2},{z,-2,2}, VectorScaling -> Automatic, VectorSizes -> Automatic]

[그림 4]와 같이 $y=0$ 평면에서의 VectorPlot을 정확히 볼 수 있어요.

중심에서 함수값이 가장 작고 중심에서 멀어질수록 함수값이 균질하게 커지고 있음을 알 수 있어요.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]