Last Updated on 2023-01-05 by BallPen
Origin 프로그램을 이용해 FFT 분석을 해보고, 제공하는 분석 정보들이 각각 무엇인지 알아봐요.
FFT 분석은 신호처리 분야에서 많이 사용되는데요. 그 이유는 분석 대상 신호에 기여하는 사인꼴 파형의 주파수(frequency)와 진폭(amplitude)을 쉽게 구할 수 있기 때문입니다.
FFT 분석을 위해, 특히 과학분야에서는 OriginLab의 오리진(Origin) 프로그램이 많이 활용되고 있어요.
이번 글은 그 Origin 프로그램으로 어느 신호의 FFT 분석을 해보고, 제공하는 분석 정보들이 각각 무슨 의미를 갖는지 알아보겠습니다. Origin 말고 다른 프로그램을 사용하더라도 분석 결과는 거의 비슷하니 도움이 될거에요.
아래는 이번 글의 목차입니다.
Contents
1. 시간 영역(time domain, 시간 도메인) 신호
시간 영역 신호란 시간의 함수로 표현되는 신호를 말합니다. 어느 신호가 있을 때 가로축(x축)이 시간으로 되어 있으면 그게 바로 시간 영역 신호인 것입니다.
예를 들기 위해 임의의 신호를 하나 만들었는데요.
아래 [그림 1]은 x축이 초(s) 단위를 갖는 시간(time)이고, y축은 볼트(V) 단위를 갖는 전압(voltage)으로 만들어진 순서쌍을 보여주고 있어요. 바로 이것이 시간 영역 신호가 될 수 있습니다.
![[그림 1] FFT 분석 예시를 위해 <span class="katex-eq" data-katex-display="false">x</span>좌표가 시간으로 주어진 순서쌍](https://ballpen.blog/wp-content/uploads/2022/06/Screen-Shot-2022-06-01-at-8.00.08-PM.png)
이 시간영역 순서쌍에서는 x축의 샘플링 시간 간격(sampling interval) \Delta t는 0.01 s 입니다. 즉 0.01 s 마다 측정이 이루어진 것으로 보면 됩니다.
\tag{1}
\Delta t = 0.01~\mathrm{s} 아울러 [그림 1]에 보이지는 않습니다만, 이 순서쌍에서 x축의 시간 최대값 t_{max}은 0.01 s 간격으로 5.00 s까지 이어져 있어요.
\tag{2}
t_{max} = 5.00~\mathrm{s}그러므로 신호 길이의 척도인 총 데이터 갯수 N은 500개입니다.
\tag{3}
N=500또한 [그림 1]의 y축 전압값은 제가 임의로 만든 함수의 함수값입니다. 그 함수는 다음과 같이 세개의 싸인꼴 함수가 합해져 있어요.
\tag{4}
\begin{align}
y &=A_1 \sin{(2 \times\pi \times f_1 \times t) }+A_2 \cos{(2 \times\pi \times f_2 \times t)}\\
&~~~~~~~~~~~~~~~+A_3 \sin{(2 \times\pi \times f_3 \times t)}\\
&=0.80 \sin{(2 \times\pi \times 2.00 \times t) }+0.45 \cos{(2 \times\pi \times 5.00 \times t)}\\
&~~~~~~~~~~~~~~~+0.96 \sin{(2 \times\pi \times 7.00 \times t)}\\
\end{align}식(4)에서 A_1, A_2, A_3는 각 싸인꼴 신호의 진폭이고, f_1, f_2, f_3는 주파수입니다. 마지막으로 t는 [그림 1]의 x축 값에 해당합니다.
예를 들어 [그림 1]에서 맨 처음 데이터인 t=0.01에서 y=0.93699가 나온 계산은 다음과 같습니다.
\tag{5}
\begin{align}
y &=0.80 \sin{(2 \times\pi \times 2.00 \times 0.01) }+0.45 \cos{(2 \times\pi \times 5.00 \times 0.01)}\\
&~~~~~~~~~~~~~~~+0.96 \sin{(2 \times\pi \times 7.00 \times 0.01)}\\
&=0.93699
\end{align}이제 [그림 1]의 순서쌍을 그래프로 그려볼까요. 바로 아래의 [그림 2]와 같습니다.
![[그림 2] FFT 분석 예시를 위한 전압 신호의 시간 영역 그래프](https://ballpen.blog/wp-content/uploads/2022/06/Graph18-1024x791.png)
상당히 복잡한 모양의 파형을 갖고 있어요. 사실 이 시간 영역 그래프만 보아서는 파형을 구성하는 싸인꼴 신호의 진폭과 주파수를 추정하기 어렵습니다.
이때 FFT 분석을 수행하면 [그림 2]의 파형을 구성하는 싸인꼴 신호의 진동수와 진폭을 구할 수 있답니다. FFT가 제대로 동작한다면 식 (3)에서 주어진 것처럼 2.00 Hz의 진동수에서 진폭이 0.80 V, 5.00 Hz에서 진폭이 0.45 V, 7.00 Hz에서 진폭이 0.96 V가 나와야 할거에요.
정말 이러한 값들이 나오는지 Origin 프로그램으로 FFT 분석을 해보고 그 결과를 보겠습니다.
2. FFT 분석 예시
Origin 프로그램으로 [그림 2]의 신호를 FFT 분석해 보았어요. 분석을 시작할 때 sampling Interval을 지정해야하는데요. 이 값은 (1)식의 0.01을 뜻하는 거에요.
또한 FFT 옵션에서 Spectrum type을 지정할 수 있는데요. 이 글에서는 One-sided 스펙트럼 유형을 선택했다는 가정하에서 기술하였습니다.
2-1. FFT 분석 정보
아래 [그림 3]은 FFT 분석으로 도출된 데이터입니다. 가장 왼쪽 열이 주파수(frequency)이고, amplitude라고 쓰여 있는 열이 바로 진폭에 해당합니다. 그러면 정말로 2 Hz 진동수에서 진폭이 0.80 V, 5 Hz에서 진폭이 0.45 V, 7 Hz에서 진폭이 0.96 V가 나오는지 확인해 봐요.
![[그림 3] FFT 분석 결과 화면. [그림 1]의 순서쌍을 FFT 분석하면 Frequency, Complex, Real 등의 다양한 정보들이 나타납니다.](https://ballpen.blog/wp-content/uploads/2022/06/Screen-Shot-2022-06-01-at-7.56.58-PM-1024x609.png)
그림을 보면 빨강색 사각형으로 표시한 것처럼 frequency가 2 Hz에서 amplitude가 0.8(파랑색 사각형 부분)이 나온것을 알 수 있어요. 또한 5 Hz에서 amplitude가 0.45로 나온 것도 알 수 있어요. 그리고 [그림 3]에서는 확인할 수 없으나 7 Hz에서 amplitude는 0.96으로 나온답니다.
이 세 수치를 제외한 나머지 amplitude 값들은 0이거나 0에 아주 가깝게 나와 기여가 거의 없다는 것을 알 수 있어요.
결국 어느 신호를 FFT 분석하면 그 신호에 기여하는 싸인꼴 함수의 주파수와 진폭 등을 알 수 있게 됩니다.
이쯤되면 FFT 분석이 매우 유용하다는 것을 알았을 텐데요. 그런데 [그림 3]에는 amplitude 말고도 다른 정보들이 기록되어 있어요. 각각의 의미를 알아보겠습니다.
[Frequency, 주파수]
시간영역 신호를 FFT 분석하면 얻어지는 주파수 값입니다. [그림 3]을 보면 주파수가 0, 0.2, 0.4 …으로 주어져 있어요. 이때 이웃한 주파수 사이의 간격인 \Delta f가 0.2 Hz로 주어지는데요. 다음의 식으로 계산된 것입니다.
\tag{6}
\begin{align}
\Delta f &= {{1}\over{\Delta t \times N}}\\
&={{1}\over{0.01~\mathrm{s} \times500}}\\
&={{1}\over{5~\mathrm{s}}}\\
&=0.2 ~\mathrm{Hz}
\end{align}여기서 \Delta f는 주파수 해상도 또는 주파수 분해능으로 불립니다. 그 이유는 이 값이 작을 수록 더욱 촘촘하게 주파수에 따른 특징들을 알 수 있기 때문입니다. \Delta f를 작게함으로써 주파수 해상도를 높이기 위해서는 (6)식과 같이 신호의 크기 N을 늘려주어야 합니다. 다만 컴퓨터의 연산속도는 데이터가 많아지므로 느려집니다.
또한 주파수 열의 가장 끝 값인 최대 주파수 f_{max}은 (7)식과 같이 주어집니다. 이 식은 (6)식을 N배한 후 2로 나눠준 형태입니다. 여기서 2로 나누는 이유는 스펙트럼 유형을 어떻게 설정하느냐에 의존하는데요. One-sided 스펙트럼의 경우에는 2로 나누어주어야 합니다.
\tag{7}
\begin{align}
f_{max} &= {{{{N}\over{\Delta t \times N}}}\over{2}}\\
&={{{{1}}}\over{2\Delta t}}\\
&={{{{1}}}\over{2 \times 0.01}}\\
&=50~\mathrm{Hz}
\end{align}위 식에 따르면 \Delta t가 작을수록 f_{max}은 증가합니다.
[Complex, 복소수]
FFT 분석을 하면 (6)식의 주파수 간격 마다 FFT 결과인 복소수 값이 얻어집니다. ‘Complex’는 바로 그 복소수 값을 보여주는 거에요. 복소수는 실수부와 허수부가 결합되어 있습니다.
예를 들어 [그림 3]에서 2 Hz에 대한 FFT 데이터는 25.06665-198.42294i로 주어졌어요.
시간 영역 순서쌍이 어떻게 FFT 복소수 데이터로 바뀌는지에 대해서는 여기를 클릭하시면 해당 글로 이동합니다.
[Real, 실수부]
‘Real’은 바로 앞에서 설명드렸던 ‘complex’에 기록된 FFT 복소수 데이터의 실수부 값입니다.
예를 들어 2 Hz에 대한 FFT 데이터는 25.06665-198.42294i인데요. 여기서 앞에 있는 실수부를 떼내어 25.06665만을 표기한 것입니다.
[Imaginary, 허수부]
‘Imaginary’은 앞에서 설명드린 ‘complex’에서의 허수부 값입니다.
예를 들어 2 Hz에 대한 FFT 결과는 25.06665-198.42294i인데요. 여기서 뒤에 있는 허수부를 떼내어 -198.42294만을 표기한 것입니다.
[Magnitude, 크기]
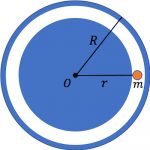
‘Magnitude’란 FFT로 얻어진 복소수 값의 크기를 말합니다. 복소평면에서는 가로축을 실수축, 세로축을 허수축으로 둡니다. 그때 복소수는 복소평면에서의 한 점을 뜻하며 원점으로부터 그 점까지의 길이가 바로 크기 r입니다.
![[그림 4] 복소평면에서 복소수는 한 지점의 위치를 나타냅니다. 이때 원점에서 그 지점까지의 길이를 크기(magnitude)라고 합니다](https://ballpen.blog/wp-content/uploads/2022/06/Complex_conjugate_picture.png)
피타고라스 정리를 사용하면 그 크기를 구할 수 있죠.
예를 들어 2 Hz에 대한 FFT 데이터는 25.06665-198.42294i인데요. 피타고라스 정리를 이용하여 빗면의 길이를 구하는 방법을 그대로 적용하면 됩니다.
\tag{8}
\begin{align}
r &= \sqrt{\mathrm{Real}^2 + \mathrm{Imaginary}^2}\\
&=\sqrt{(25.06665)^2 + (-198.42294)^2}\\
& = 200~\mathrm{V}
\end{align}[그림 3]에서와 동일하게 200이 도출되었습니다.
[Amplitude, 진폭]
‘Amplitude’란 앞에서 설명한 것처럼 싸인꼴 함수의 진폭을 뜻합니다. 크기(magnitude) r을 N으로 나눈 값을 A^{\prime}이라고 했을 때 진폭 A는 A^{\prime}에 2를 곱하여 계산합니다. 2 Hz의 경우에 대해 계산해보겠습니다.
\tag{9}
\begin{align}
A&=2\times A^{\prime}=2 \times{{r}\over{N}}=2\times{{\sqrt{\mathrm{Real}^2 + \mathrm{Imaginary}^2}}\over{N}}\\
&=2 \times{{200}\over{500}}\\
&=0.8~\mathrm{V}
\end{align}[그림 3]에서와 동일하게 0.8이 나왔습니다.
[Phase, 위상]
[그림 4]에서 복소수 x+iy가 있을 때 \tan \phi = {{y}/{x}}로 주어집니다.
그러므로 \phi는 다음과 같이 계산할 수 있어요. 여기서도 2 Hz의 경우 복소수가 25.06665-198.42294i로 주어지므로 이것을 이용해 계산해 보겠습니다.
\tag{10}
\begin{align}
\phi &= \tan^{-1} {{\mathrm{Imaginary}}\over{\mathrm{Real}}}\\
&= \tan^{-1} {{-198.42294}\over{25.06665}}\\
&=-82.8^{\circ}\\
&=277.2^{\circ}
\end{align}[그림 3]에서와 동일하게 277.2^{\circ}가 나왔습니다.
[Power as MSA]
진동자가 진동할 때 진동 진폭 A의 제곱은 진동자의 총 에너지에 비례합니다. 주파수의 함수로서 총 에너지 관계를 보여주기 위해 MSA를 사용하는데요. MSA는 Mean Squared Amplitude의 약자입니다.
다음과 같이 크기(magnitude) r을 N으로 나눈 값을 A^{\prime}이라고 했을 때, A^{\prime}을 제곱한 후 2를 곱하여 구합니다.
2 Hz의 경우 계산해보면 [그림 3]과 같이 0.32가 얻어집니다.
\tag{11}
\begin{align}
\mathrm{Power~ as~ MSA} &= 2 (A^{\prime})^2\\
&=2\times{{\sqrt{\mathrm{Real}^2 + \mathrm{Imaginary}^2}}^2\over{N^2}}\\
&=2\times{{{\mathrm{Real}^2 + \mathrm{Imaginary}}}^2\over{N^2}}\\
&=2 \times{{25.06665^2}+{(-198.42294)^2}\over{500^2}}\\
&=0.32~\mathrm{V^2}
\end{align}[dB, 데시벨]
주파수의 함수로서 진폭을 그래프로 표현할 때 큰 진폭은 그래프에서 명확히 보이겠지만 아주 작은 진폭은 잘 보이지 않을 거에요. 그래서 작은 진폭도 잘 보이도록 진폭 A에 로그를 취한 것을 데시벨(dB)이라 합니다. 로그의 성질을 이용해 작은 진폭도 잘 보이도록 하는 거에요.
계산은 다음의 식을 이용하는데요. 2 Hz의 경우에 대해 계산해보겠습니다.
\tag{12}
\begin{align}
{dB} &=20 \log(A)\\
&=20 \log (0.8)\\
&=-1.9382~\mathrm{dB}
\end{align}[그림 3]에서와 동일하게 -1.9382~\mathrm{dB}이 나왔습니다.
2-2. 주파수 영역(frequency domain, 주파수 도메인)
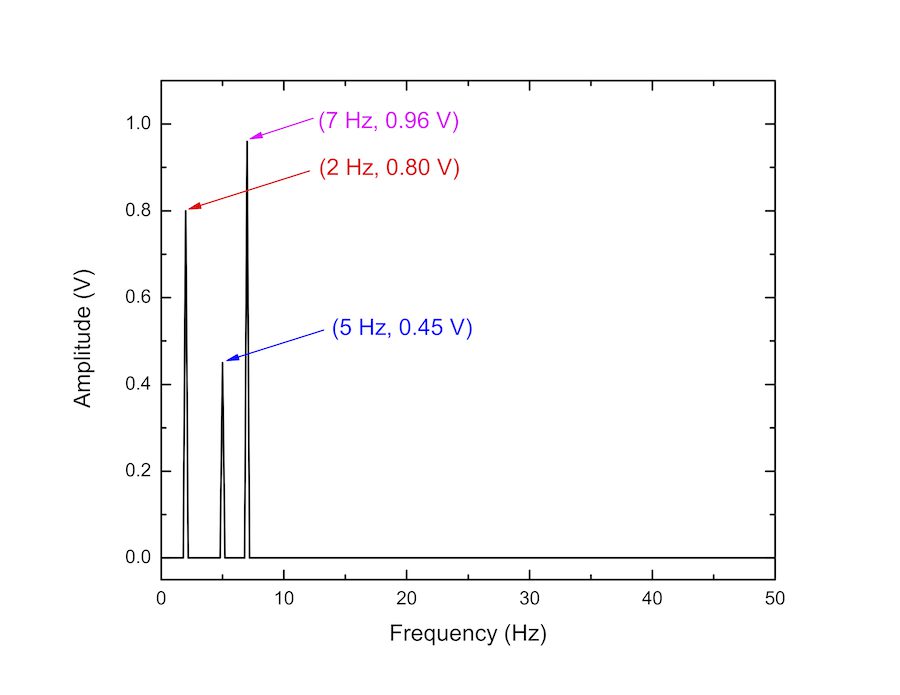
아래 [그림 5]는 [그림 3]에 주어진 FFT 데이터들 중에서 frequency와 amplitude를 선택하여 그린 FFT 그래프입니다. 이러한 그래프를 다른 말로 FFT 스펙트럼이라고도 부릅니다.
![[그림 5] FFT 분석 그래프. [그림 3]의 데이터에서 <span class="katex-eq" data-katex-display="false">x</span>축을 frequency, <span class="katex-eq" data-katex-display="false">y</span>축을 amplitude로 선택하여 그린 주파수 영역 그래프](https://ballpen.blog/wp-content/uploads/2022/06/Graph19-1024x791.png)
그림과 같이 원래 신호에 기여하는 싸인꼴 함수의 주파수에서 봉우리가 형성되어 나타남을 알 수 있습니다.
3. 신호 길이와 주파수 영역의 관계
지금까지 시간 영역 신호를 FFT 분석하여 주파수 영역 신호로 변환하고 분석하는 과정을 설명드렸습니다. 이번에는 \Delta t는 0.01 s로 고정하되, t_{max}을 10.0 s로 확장함으로써 신호 길이 N이 총 1000개가 되는 시간 영역 데이터를 분석해 보아요.
즉, 아래의 [그림 6]은 신호 길이가 [그림 2]의 두배인 시간 영역 그래프입니다. 나머지 조건은 모두 동일합니다.
![[그림 6] 신호 길이 <span class="katex-eq" data-katex-display="false">N</span>이 [그림 2]의 두배인 시간 영역 그래프](https://ballpen.blog/wp-content/uploads/2022/06/Graph9-1024x791.png)
[그림 6]의 신호를 FFT 분석하면 어떻게 달라질까요? 아래 [그림 7]은 FFT 스펙트럼 결과에요.
![[그림 7] 신호 길이 <span class="katex-eq" data-katex-display="false">N</span>이 [그림 2]의 두배인 경우에 대한 FFT 스펙트럼. 이 그래프는 <span class="katex-eq" data-katex-display="false">x</span>축이 주파수이기 때문에 주파수 영역 그래프라고 부릅니다.](https://ballpen.blog/wp-content/uploads/2022/06/Graph8-1024x791.png)
신호 길이 N이 두배가 되면 FFT 스펙트럼에서 \Delta f가 아래 (13)식과 같이 이전보다 1/2이 작아집니다. 즉 신호길이가 증가하면 주파수 해상도가 향상되는거에요.
\tag{13}
\begin{align}
\Delta f &= {{1}\over{\Delta t \times N}}\\
&={{1}\over{0.01~\mathrm{s} \times1000}}\\
&={{1}\over{10~\mathrm{s}}}\\
&=0.1 ~\mathrm{Hz}
\end{align}따라서 [그림 5]에 비해 [그림 7]의 FFT 스펙트럼에서 봉우리의 반치폭(FWHM)이 더 좁게 나타나는 것을 알 수 있어요.
다만 주파수 해상도는 증가하지만 최대 주파수 값 f_{max}은 아래 (14)식과 같이 변하지 않아요.
\tag{14}
\begin{align}
f_{max} &= {{{{N}\over{\Delta t \times N}}}\over{2}}\\
&={{{{1}}}\over{2\Delta t}}\\
&={{{{1}}}\over{2 \times 0.01}}\\
&=50~\mathrm{Hz}
\end{align}f_{max}을 더 늘리기 위해서는 시간 영역 데이터에서 \Delta t가 더 작아야 합니다. 즉 측정을 더 빠른 시간 간격으로 해야만 f_{max}이 증가해요.







아… 아주 큰 도움 되었습니다.
최고네요 진짜..
“시간 영역 순서쌍이 어떻게 FFT 복소수 데이터로 바뀌는지에 대해서는 다른 글에서 따로 다루겠습니다.” 요것도 기다리겠습니다 작성자님 ㅎㅎ
방문해 주셔서 감사합니다. 도움이 되었다니 다행입니다.
시간 영역 순서쌍을 FFT 데이터로 바꾸는 내용의 링크를 본문 글에 추가하였습니다.
빨강색 글씨로 되어있는 부분을 보시면 링크가 연결되어 있는게 보일거에요.
감사합니다.
앗 감사합니다. 죄송한데 한가지만 더 여쭤봐도 될까요.
[그림1]에 예제에서 [그림2]의 FFT의 복소수 값을 프로그램 통하지 않고 손으로도 계산할 수 있을까요 ??
네, 복잡하기는 하지만 손으로도 계산할 수 있어요.
위에서 말씀드렸던 링크를 타고 들어가시면 손으로 계산하는 방법이 있습니다.
이 글의 본문에서 빨간색 글씨 부분에 “여기를 클릭하시면 해당 글로 이동합니다” 부분을 클릭하면 됩니다.