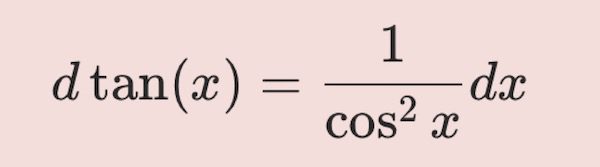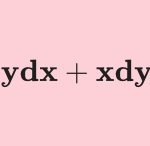Last Updated on 2025-09-02 by BallPen
\tan(x) 미분 방법을 알아 봐요.
\tan(x)를 x로 미분해 봐요.
\begin{align*}
{{d\tan(x)}\over{dx}} &= {d \over dx} \Big({{\sin x}\over{\cos x}}\Big)\\[10pt]
&={{d}\over{dx}}(\sin x (\cos x)^{-1})\\[10pt]
&=\cos x (\cos x)^{-1} + \sin x (-1)(\cos x)^{-2}(-\sin x)\\[10pt]
&=1+{{\sin^2 x}\over{\cos^2 x}}\\[10pt]
&={{\cos^2 x + \sin^2 x}\over{\cos^2 x}}\\[10pt]
&={1 \over{\cos^2 x}}
\end{align*}윗 식의 두번째 줄에서 세번째 줄로 넘어갈 때 곱의 미분 규칙이 적용되었습니다.
결국 다음의 관계가 성립합니다.
\begin{align*}
d \tan (x) = {1 \over {\cos^2 x}} dx
\end{align*}흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 1 Average: 5]