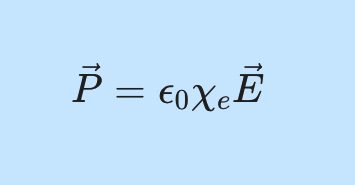Last Updated on 2025-10-17 by BallPen
선형 유전체 속의 전기장과 편극밀도, 전기변위 사이의 관계를 알아 봐요.
선형 유전체(linear dielectrics)란 무엇이고, 그 유전체 속의 전기장 \vec E와 편극밀도 \vec P 사이의 관계, 그리고 이로 인해 선형유전체의 전기변위 \vec D가 어떻게 달라지는지 알아봐요.
주요 식을 결과부터 쓰면 다음과 같아요.
\tag{D1}
\vec P = \epsilon_0 \chi_e \vec E\tag{D2}
\vec D = \epsilon_0(1+\chi_e) \vec E = \epsilon \vec E아울러 유전체의 전기감수율, 유전율, 유전상수 개념에 대해서도 알아봐요. 아래는 이번 글의 목차입니다.
1. 선형 유전체
전기장이 너무 강하지 않으면 많은 유전체는 편극밀도 \vec P가 유전체 내부의 전기장 \vec E에 비례합니다.
이를 식으로 표현하면 다음과 같아요.
\tag{1-1}
\vec P = \epsilon_0 \chi_e \vec E여기서 중요한 것은 윗 식에 있는 전기장 \vec E가 최초 편극을 유도한 전기장 \vec E_0가 아니라는 거에요.
무슨 말이냐면 \vec E_0에 의해 유전체가 최초 편극되면 그 편극에 의해 추가적인 전기장이 생기고, 그 추가적 전기장이 추가적인 편극을 유도하는 과정이 반복될 것을 생각할 수 있을거에요. 그러다보면 결국 유전체 내의 전기장은 최종값 \vec E에 도달하게 되고 그 전기장에 의해 유전체는 최종 편극 \vec P를 갖게 됩니다.
또한 (1-1)식에서 \chi_e는 전기 감수율(electric susceptibility)이라고 부르며 유전체의 종류, 또는 온도 등에 의존하는 특성값이라고 이해하시면 좋습니다.
물론 \chi_e가 0이면 유전체가 없다는, 즉 진공상태를 뜻하고 (1-1)식에 따라 편극밀도는 \vec P = 0이 성립하게 되겠죠.
(1-1)식을 만족하는 물질을 ‘선형 유전체’ 라고 부릅니다.
2. 전기 변위, 유전율, 상대 유전율
2-1. 전기 변위
유전체의 가우스법칙에서 정의되는 전기변위 \vec D는 다음과 같이 주어집니다.
\tag{2-1}
\vec D = \epsilon_0 \vec E + \vec P윗 식에서 전기장 \vec E는 (1-1)식의 유전체 내의 전기장 \vec E와 같아요.
(1-1)식을 (2-1)식에 대입하면 전기변위 \vec D는 다음과 같이 정리할 수 있어요.
\tag{2-2}
\begin{aligned}
\vec D &= \epsilon_0 \vec E + \epsilon_0 \chi_e \vec E\\[10pt]
&=\epsilon_0(1+\chi_e)\vec E
\end{aligned}2-2. 유전율
(2-2)식의 두번째 줄에서 \epsilon_0 (1+ \chi_e )는 모두 상수입니다. 그래서 이를 다른 \epsilon기호로 치환하면 유전체 내의 전기변위인 (2-2)식은 다음과 같이 쓸 수 있어요.
\tag{2-3}
\vec D = \epsilon \vec E이때 \epsilon을 물질의 유전율(permitivity)이라고 부릅니다.
한편 위에서 말씀드렸듯이 전기 감수율이 \chi_e = 0이면 진공상태를 뜻하고 그러면 (2-2)식에 따라 진공상태에서의 전기변위는 다음과 같아요.
\tag{2-4}
\vec D = \epsilon_0 \vec E_02-3. 상대 유전율(유전상수)
앞서 물질의 유전율을 다음과 같이 정의했어요.
\tag{2-5}
\epsilon = \epsilon_0(1+\chi_e)윗 식의 형태를 조금만 바꾸면 물질과 진공의 유전율의 비율 \epsilon_r을 구할 수 있는데요.
\tag{2-6}
\epsilon_r = {{\epsilon}\over{\epsilon_0}} = 1+ \chi_e이때 그 비율인 \epsilon_r을 상대 유전율(relative permitivity) 또는 유전상수(dielectric constant)라고 부릅니다.
대표적인 몇가지 물질의 유전상수는 다음과 같아요. 이때 유전상수는 비율값이므로 단위는 없어요.
| 물질 | 유전상수 | 물질 | 유전상수 |
|---|---|---|---|
| 진공 | 1 | 벤젠 | 2.28 |
| 헬륨 | 1.000065 | 금강석 | 5.7-5.9 |
| 네온 | 1.00013 | 소금 | 5.9 |
| 수소(H2) | 1.000254 | 규소 | 11.7 |
| 건조한 공기 | 1.000536 | 메틸알코올 | 33.0 |
일단 기억할 것은 진공의 유전율이 가장 작은 값 1을 가지며, 다른 물질의 유전율은 1보다는 모두 크다는 거에요.
3. 선형 유전체 내의 전기장
진공중에서 자유 점전하 q로부터 r만큼 떨어진 곳의 전기장은 다음과 같습니다.
\tag{3-1}
\vec E_0 = {1 \over {4 \pi \epsilon_0}} {q \over r^2} \hat r그런데 만일 점전하가 유전상수가 \epsilon_r인 선형유전체로 둘러싸여 있을 때 r만큼 떨어진 유전체 내의 전기장은 다음과 같아요.
\tag{3-2}
\begin{aligned}
\vec E &= {1 \over {4 \pi \epsilon}} {q \over r^2} \hat r \\[10pt]
&= {1 \over {4 \pi \epsilon_0 \epsilon_r}} {q \over r^2} \hat r\\[10pt]
&={1 \over{\epsilon_r}} \vec E_0
\end{aligned}결국 선형 유전체 내의 전기장 \vec E은 진공중의 전기장 \vec E_0에 비해 {{1}\over{\epsilon_r}}배 만큼 항상 감소하게 됩니다.