Last Updated on 2024-01-06 by BallPen
간단한 예제를 통해 이산 푸리에 변환의 계산 방법을 알아보겠습니다.
이산 푸리에 변환(DFT, Discrete Fourier Transform)이란 시간 도메인(time domain)의 이산 신호를 주파수 도메인(frequency domain)의 이산 신호로 바꾸는 방법을 말합니다.
여기서 도메인이라 함은 그래프를 그렸을때 x축이 시간축으로 되어 있는 신호를 시간 도메인, 주파수 축으로 되어 있는 신호를 주파수 도메인이라고 합니다. 보다 자세한 내용은 이전 글을 참조해 주세요.
또한 이산 신호란 연속적인 신호와 달리 데이터가 띄엄띄엄 존재합니다. 보통은 연속적인 신호에서 주기적으로 데이터를 추출하는 샘플링과정을 통해 이산 신호를 만듭니다.
신호처리 분야에서는 이산 신호의 주파수 성분을 알기 위해 이산 푸리에 변환을 많이 하는데요.
그런데 이산 푸리에 변환의 공식이 복잡해서 직관적으로 이해하기 쉽지 않아요. 또한 푸리에 변환 결과를 보았을때 왜 저런 값이 나오게 되는지 이해가 안가는 경우도 많아요.
이때는 간단한 예제를 풀어보는 것이 큰 도움이 됩니다.
노트를 펴고 함께 해봐요. 이산 푸리에 변환 계산에 대한 자신감이 생길거에요.
아래는 이번 글의 목차입니다.
1. 이산 신호 데이터
아래 [표 1]은 이산 푸리에 변환 예제를 위해 시간 도메인의 이산 신호 데이터를 임의로 만든거에요.
| t | x_n |
|---|---|
| 1 s | 1+1i |
| 2 s | -1+2i |
| 3 s | -1 |
| 4 s | 2-1i |
두개의 열로 구성되어 있는데 왼쪽 열은 시간 t, 오른쪽 열은 신호값 x_n입니다.
x_n데이터의 총 갯수 N은 4개입니다. 그리고 데이터의 시간 간격 \Delta t는 1초에요. 이산 푸리에 변환에서는 주어진 이산 신호의 가장 끝 시간 데이터 값을 신호의 주기값 T로 간주합니다. 이때 T는 다음 (1)식으로 구해요.
\tag{1}
T=\Delta t \times N(1)식을 적용하면 [표 1] 데이터의 경우 T=1~\mathrm{s} \times 4 = 4~\mathrm{s}가 됩니다. 만일 \Delta t가 0.1초이고 N이 250개인 경우 T=0.1~\mathrm{s} \times 250 = 25~\mathrm{s}가 되겠죠.
신호값 x_n은 복소수가 될 수 있어요. 물론 실수도 가능합니다. 복소수에서 허수부가 0인 경우에는 실수가 되죠. [표 1]에서 세번째 행의 -1이 실수 신호값에 해당합니다.
이제 [표 1]의 데이터에 대해 이산 푸리에 변환을 해 볼건데요. 그 전에 이산 푸리에 변환 공식을 먼저 알아보겠습니다.
2. 이산 푸리에 변환 공식
이산 푸리에 변환 공식은 다음 (2)식과 같이 주어집니다. 이 식을 통해 시간 도메인의 복소수 값이 주파수 도메인의 복소수 값으로 변환됩니다.
\tag{2}
\begin{align}
X_k &= \sum_{n=0}^{N-1} x_n \cdot e^{-i 2 \pi {k \over T}n }\\
&= \sum_{n=0}^{N-1} x_n \cdot \Big[ \cos \big( 2 \pi {k \over T} n \big) - i \sin \big( 2 \pi {k \over T} n \big) \Big]
\end{align}(2)식에서 X_k는 주파수 도메인으로 변환된 복소수이고, x_n은 시간 도메인에서의 복소수입니다. 즉 [표 1]의 x_n에 해당합니다.
그리고 T는 (1)식으로 주어진 입력신호의 최대 주기값입니다. 일부 책에서 T대신에 N으로 표기하는 경우가 있는데요. 그것은 \Delta t = 1인 경우에 해당합니다.
아울러 (2)식에서 보이는 k \over T가 주파수 도메인에서의 주파수 f에 해당합니다.
그렇다면 이번에는 주파수 도메인의 복소수 X_k를 시간 도메인의 복소수 x_n으로 원래대로 다시 바꾸기 위해서는 어떻게 해야 할까요? 바로 역변환(inverse transform)을 해주면 됩니다.
그 공식은 아래 (3)식과 같아요.
\tag{3}
\begin{align}
x_n &= {1 \over T} \sum_{k=0}^{N-1} X_k \cdot e^{i 2 \pi {k \over T}n}\\
&={1 \over T} \sum_{k=0}^{N-1} X_k \cdot \Big[ \cos \big( 2 \pi {k \over T} n \big) + i \sin \big( 2 \pi {k \over T} n \big) \Big]
\end{align}(2)식과 (3)식은 간단해 보이면서도 복잡해보이기도 합니다.
이제 이산 푸리에 변환을 해보겠습니다.
3. 이산 푸리에 변환 계산 예제
[표 1]에 주어진 시간 도메인의 복소수 x_n을 주파수 도메인의 복소수 X_k로 바꾸어 보겠습니다.
(2)식을 적용하면 됩니다.
가장 먼저 f={0 \over 4}=0.00~\mathrm{Hz}에서의 X_0입니다.
\tag{4}
\begin{align}
X_0 &= (1+i)\cdot e^{-i2 \pi {0 \over 4}0} +(-1+2i) \cdot e^{-i2 \pi {0 \over 4}1}\\
&~~~~~~~~~+(-1+0i) \cdot e^{-i2 \pi {0 \over 4}2}+(2-1i) \cdot e^{-i2 \pi {0 \over 4}3}\\
&=(1+i)\cdot \big[\cos (2 \pi {0 \over 4}0)-i\sin(2 \pi {0 \over 4}0)\big]\\
&~~~~~~~~~+(-1+2i)\cdot \big[\cos (2 \pi {0 \over 4}1)-i\sin(2 \pi {0 \over 4}1)\big]\\
&~~~~~~~~~+(-1+0i)\cdot \big[\cos (2 \pi {0 \over 4}2)-i\sin(2 \pi {0 \over 4}2)\big]\\
&~~~~~~~~~+(2-1i)\cdot \big[\cos (2 \pi {0 \over 4}3)-i\sin(2 \pi {0 \over 4}3)\big]\\
&=(1+i)\cdot(1-0i)\\
&~~~~~~~~~+(-1+2i)\cdot(1-0i)\\
&~~~~~~~~~+(-1+0i)\cdot(1-0i)\\
&~~~~~~~~~+(2-1i)\cdot(1-0i)\\
&=(1+i)+(-1+2i)+(-1+0i)+(2-1i)\\
&=1+2i
\end{align}전개과정이 상당히 재미있어요. 이번에는 f={1 \over 4}=0.25~\mathrm{Hz}에서의 X_1입니다.
\tag{5}
\begin{align}
X_1 &= (1+i)\cdot e^{-i2 \pi {1 \over 4}0} +(-1+2i) \cdot e^{-i2 \pi {1 \over 4}1}\\
&~~~~~~~~~+(-1+0i) \cdot e^{-i2 \pi {1 \over 4}2}+(2-1i) \cdot e^{-i2 \pi {1 \over 4}3}\\
&=(1+i)\cdot \big[\cos (2 \pi {1 \over 4}0)-i\sin(2 \pi {1 \over 4}0)\big]\\
&~~~~~~~~~+(-1+2i)\cdot \big[\cos (2 \pi {1 \over 4}1)-i\sin(2 \pi {1 \over 4}1)\big]\\
&~~~~~~~~~+(-1+0i)\cdot \big[\cos (2 \pi {1 \over 4}2)-i\sin(2 \pi {1 \over 4}2)\big]\\
&~~~~~~~~~+(2-1i)\cdot \big[\cos (2 \pi {1 \over 4}3)-i\sin(2 \pi {1 \over 4}3)\big]\\
&=(1+i)\cdot(1-0i)\\
&~~~~~~~~~+(-1+2i)\cdot(0-1i)\\
&~~~~~~~~~+(-1+0i)\cdot(-1-0i)\\
&~~~~~~~~~+(2-1i)\cdot(0+1i)\\
&=(1+1i)+(2+1i)+(1+0i)+(1+2i)\\
&=5+4i
\end{align}이번에는 f={2 \over 4}=0.50~\mathrm{Hz}에서의 X_2입니다.
\tag{6}
\begin{align}
X_1 &= (1+i)\cdot e^{-i2 \pi {2 \over 4}0} +(-1+2i) \cdot e^{-i2 \pi {2 \over 4}1}\\
&~~~~~~~~~+(-1+0i) \cdot e^{-i2 \pi {2 \over 4}2}+(2-1i) \cdot e^{-i2 \pi {2 \over 4}3}\\
&=(1+i)\cdot \big[\cos (2 \pi {2 \over 4}0)-i\sin(2 \pi {2 \over 4}0)\big]\\
&~~~~~~~~~+(-1+2i)\cdot \big[\cos (2 \pi {2 \over 4}1)-i\sin(2 \pi {2 \over 4}1)\big]\\
&~~~~~~~~~+(-1+0i)\cdot \big[\cos (2 \pi {2 \over 4}2)-i\sin(2 \pi {2 \over 4}2)\big]\\
&~~~~~~~~~+(2-1i)\cdot \big[\cos (2 \pi {2 \over 4}3)-i\sin(2 \pi {2 \over 4}3)\big]\\
&=(1+i)\cdot(1-0i)\\
&~~~~~~~~~+(-1+2i)\cdot(-1-0i)\\
&~~~~~~~~~+(-1+0i)\cdot(1-0i)\\
&~~~~~~~~~+(2-1i)\cdot(-1-0i)\\
&=(1+1i)+(1-2i)+(-1+0i)+(-2+1i)\\
&=-1+0i
\end{align}이번에는 f={3 \over 4}=0.75~\mathrm{Hz}에서의 X_3입니다.
\tag{7}
\begin{align}
X_1 &= (1+i)\cdot e^{-i2 \pi {3 \over 4}0} +(-1+2i) \cdot e^{-i2 \pi {3 \over 4}1}\\
&~~~~~~~~~+(-1+0i) \cdot e^{-i2 \pi {3 \over 4}2}+(2-1i) \cdot e^{-i2 \pi {3 \over 4}3}\\
&=(1+i)\cdot \big[\cos (2 \pi {3 \over 4}0)-i\sin(2 \pi {3 \over 4}0)\big]\\
&~~~~~~~~~+(-1+2i)\cdot \big[\cos (2 \pi {3 \over 4}1)-i\sin(2 \pi {3 \over 4}1)\big]\\
&~~~~~~~~~+(-1+0i)\cdot \big[\cos (2 \pi {3 \over 4}2)-i\sin(2 \pi {3 \over 4}2)\big]\\
&~~~~~~~~~+(2-1i)\cdot \big[\cos (2 \pi {3 \over 4}3)-i\sin(2 \pi {3 \over 4}3)\big]\\
&=(1+i)\cdot(1-0i)\\
&~~~~~~~~~+(-1+2i)\cdot(0+1i)\\
&~~~~~~~~~+(-1+0i)\cdot(-1-0i)\\
&~~~~~~~~~+(2-1i)\cdot(0-1i)\\
&=(1+1i)+(-2-1i)+(1+0i)+(-1-2i)\\
&=-1-2i
\end{align}지금까지 구한 결과를 하나의 표로 정리하면 아래 [표 2]와 같습니다.
| f | X_k |
|---|---|
| 0.00 Hz | 1+2i |
| 0.25 Hz | 5+4i |
| 0.50 Hz | -1+0i |
| 0.75 Hz | -1-2i |
여기서 주의해야 할 것은 Origin과 같은 푸리에 변환 프로그램을 이용하면 [표 2]의 모든 변환 결과가 나오지 않습니다. 푸리에 스펙트럼에서 보여주는 주파수의 상한 값은 보통 아래의 규칙에 따라 정해집니다.
\tag{8}
f_{max} = {1 \over 2\Delta t}그러므로 본 예시의 경우 주파수 상한 값은 f_{max} = {{1 \over {2 \Delta t}} = {1 \over {2 \times 1~\mathrm {s}}} = {0.50~\mathrm{Hz}}}가 됩니다. 따라서 FFT 분석 후의 데이터를 보면 [표 2]에서와 같이 보여지는 것이 아니라 0.00 Hz부터 0.50 Hz까지만 보여지게 됩니다.
4. 이산 푸리에 변환의 역변환
[표 2]에 주어진 주파수 도메인의 복소수 X_k를 시간 도메인의 복소수 x_n으로 다시 바꾸어 보겠습니다. 이것을 역변환이라고 하죠.
(3)식을 적용하면 됩니다.
예시로서 하나만 풀어보겠습니다. [표 2]의 X_3 =-1-2i가 역변환을 하면 [표 1]의 x_3 = 2-1i로 되돌아가는지 보겠습니다.
\tag{9}
\begin{align}
x_3 &= {1 \over 4} \Big[(1+2i)\cdot e^{i2 \pi {0 \over 4}3} +(5+4i) \cdot e^{i2 \pi {1 \over 4}3}\\
&~~~~~~~~~+(-1+0i) \cdot e^{i2 \pi {2 \over 4}3}+(-1-2i) \cdot e^{i2 \pi {3 \over 4}3}\Big]\\
&={1 \over 4}\Big[(1+2i)\cdot \big[\cos (2 \pi {0 \over 4}3)+i\sin(2 \pi {0 \over 4}3)\big]\\
&~~~~~~~~~+(5+4i)\cdot \big[\cos (2 \pi {1 \over 4}3)+i\sin(2 \pi {1 \over 4}3)\big]\\
&~~~~~~~~~+(-1+0i)\cdot \big[\cos (2 \pi {2 \over 4}3)+i\sin(2 \pi {2 \over 4}3)\big]\\
&~~~~~~~~~+(-1-2i)\cdot \big[\cos (2 \pi {3 \over 4}3)+i\sin(2 \pi {3 \over 4}3)\big]\Big]\\
&={1 \over 4}\Big[(1+2i)\cdot(1+0i)\\
&~~~~~~~~~+(5+4i)\cdot(0-1i)\\
&~~~~~~~~~+(-1+0i)\cdot(-1+0i)\\
&~~~~~~~~~+(-1-2i)\cdot(0+1i)\Big]\\
&={1 \over 4}\Big[(1+2i)+(4-5i)+(1+0i)+(2-1i)\Big]\\
&={1 \over 4}(8-4i)\\
&=2-1i
\end{align}(3)식의 역변환 공식도 성립하는 것을 알 수 있습니다.
이렇게 해서 이번 글에서는 이산 푸리에 변환과 그 역변환의 풀이에 대한 간단한 예제를 다루었습니다. 이산 푸리에 변환을 통한 FFT의 크기, 진폭, 위상 등에 대한 분석 방법은 이전 글을 참조해 주세요.

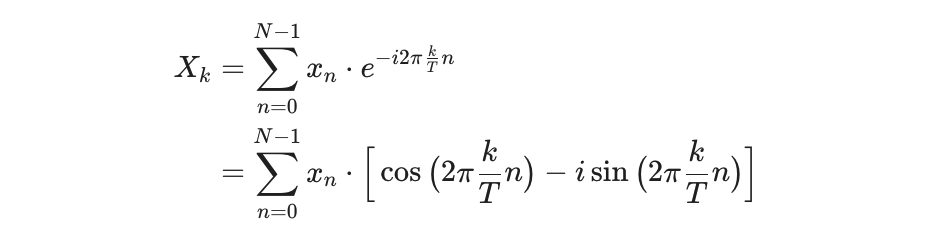




1 thought on “이산 푸리에 변환 예제”