Last Updated on 2024-03-03 by BallPen
표준 오차 계산 방법을 예제로 알아보아요.
표준 오차 계산 방법에 대한 예제입니다.
문제
어떤 물체의 질량을 측정하기 위해 다음과 같이 총 10번의 측정이 이루어졌다고 가정하겠습니다. 질량은 SI 기본 물리량으로써 측정값의 단위는 kg을 사용합니다.
| 측정번호 | 측정값(kg) | 측정번호 | 측정값(kg) |
|---|---|---|---|
| x_1 | 5.65 | x_6 | 5.78 |
| x_2 | 5.72 | x_7 | 5.43 |
| x_3 | 5.46 | x_8 | 5.50 |
| x_4 | 5.52 | x_9 | 5.83 |
| x_5 | 5.60 | x_{10} | 5.61 |
이때 신뢰수준은 95%를 적용합니다.
(a) 측정값의 표준 오차 SEM을 구하세요.
(b) 허용 오차를 이용하여 측정값을 표기하세요.
(a) 측정값의 표준 오차 계산
문제에서 주어진 데이터는 실험세트가 하나인 경우로 총 10개의 측정값으로 구성되어 있습니다.
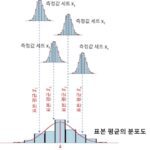
표준 오차, SEM(Standard Error of Mean)이란 표본 평균에 대한 표준 편차로 정의됩니다. 표준 오차에 대한 식은 다음과 같습니다.
\tag{1} SEM = {{\sigma}\over{\sqrt{n}}}(1)식에서 \sigma는 모집단의 표준편차이고, n은 측정횟수 입니다. 그러나 우리는 모집단의 표준편차를 모르기 때문에 측정을 통해 얻어진 표본의 표준편차 s를 모집단의 표준편차 \sigma로서 추정하게 됩니다.
따라서 (1)식은 다음과 같이 변경될 수 있습니다.
\tag{2} SEM = {{s}\over{\sqrt{n}}}
이제부터 (2)식의 표준 오차 SEM을 계산하겠습니다. 그러기 위해서는 표준 편차 s를 구해야 하는데, 이를 위해서는 측정값의 평균 \mu가 우선 필요합니다. 평균은 다음과 같습니다.
\begin{align}
\tag{3}
\mu &= {{\Sigma{x}}\over{n}} = {{x_1 + x_2 + \ldots + x_9 + x_{10}}\over{n}}\\[10pt]
&={{5.65+5.72+\ldots+5.83+5.61}\over{10}}\\[10pt]
&=5.61~\mathrm{kg}
\end{align}위에서 구해진 평균값 \mu를 이용하여 표본의 표준 편차 s를 계산합니다.
\begin{align}
\tag{4}
s &= \sqrt{{\Sigma(x-\mu)^2}\over{n-1}}\\[10pt]
&= \sqrt{{(5.65-5.61)^2 + \ldots + (5.61-5.61)^2}\over{10-1}} \\[10pt]
&= 0.136
\end{align}그러면 최종적으로 (2)식의 표준 오차 SEM은 다음과 같이 구해집니다.
\begin{align}
\tag{5}
SEM &= {{s}\over{\sqrt{n}}}\\[10pt]
&={{0.136}\over{\sqrt{10}}}\\[10pt]
&=0.043
\end{align}(b) 허용 오차와 측정값 표기
측정값을 허용 오차(margin of error)를 활용해 표기하기 위해서는 ‘평균값\pm허용오차’의 형태로 표기하면 됩니다. 이를 신뢰구간(confidence interval)이라고 합니다. 이때 측정횟수가 10개뿐이므로 t값을 활용해 허용오차를 구하는 것이 좋습니다.
\begin{align}
\tag{6}
평균값 \pm 허용오차 &= \mu \pm \Big( t_{{\alpha}\over{2}} \times {{s}\over{\sqrt{n}}} \Big) \\[10pt]
&= \mu \pm ( t_{{\alpha}\over{2}} \times {SEM})
\end{align}이미 위에서 평균값 \mu와 SEM은 구해 놓았습니다. 그렇다면 t_{{\alpha}\over{2}}만 구하면 될 것 같아요.
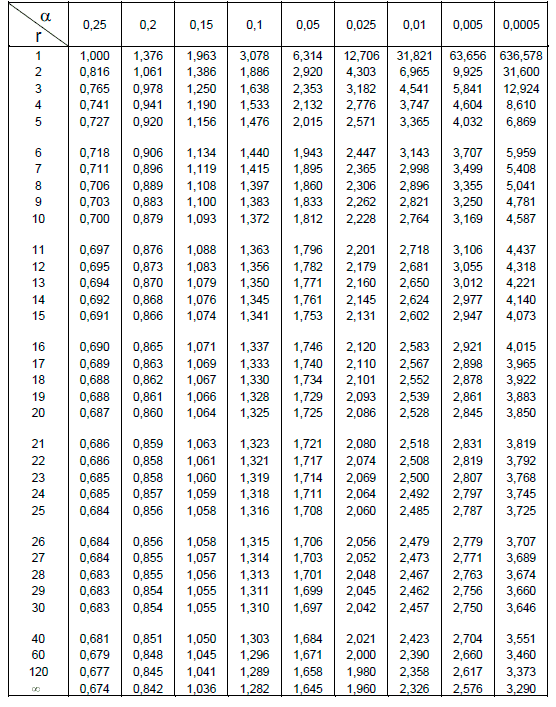
아래의 표는 t-분포표입니다.
이 표는 세로축이 r로서 표기되어 있는데 이것을 자유도(Degree of freedom)라고 합니다. 일반적으로 측정에서의 자유도 r이란 측정횟수 n에서 1을 뺀 값을 말합니다.
즉 측정을 n=10회 했을 때 자유도 r은 다음과 같이 9입니다.
r = n-1 = 10-1 = 9
t-분포표에서 가로축이 \alpha로 표시되어 있습니다. 이것은 확률을 뜻합니다.
예를 들어 연구자들이 많이 선택하는 95% 신뢰수준의 경우 \alpha는 다음 식으로 계산됩니다.
\begin{align*}
(1-\alpha) \times 100 &= 95\% \\[7pt]
1- \alpha &= {{95}\over{100}} \\[7pt]
\alpha &= 1-{{95}\over{100}} \\[7pt]
&=0.05
\end{align*}이때 \alpha는 위에서 구한 값을 그대로 사용하지 않습니다. 그 이유는 t-분포의 양 끝단에서 \alpha값을 절반씩 나누어 갖기 때문입니다. 그래서 {\alpha}\over{2}는 다음과 같습니다.
{{\alpha}\over{2}} = {{0.05}\over{2}} = 0.025
자 그러면 아래의 표를 이용해 t_{{\alpha}\over{2}}를 찾아 보겠습니다.
r=9이고, {{\alpha}\over{2}}=0.025가 교차하는 숫자를 읽으면 됩니다. 무슨 값이 나오냐면 2.262가 나옵니다.
t_{{\alpha}\over{2}} = 2.262
(출처 : By Jsmura – Own work, CC BY-SA 4.0)
결국 n=10, \mu=5.61, SEM=0.043의 신뢰 구간은 아래와 같습니다.
\begin{align*}
5.61 - (2.262 \times 0.043) \le &\mu \le 5.61 + (2.262 \times 0.043)\\
5.51 \le &\mu \le 5.71
\end{align*}또는 (6)식과 같은 형태로 표기하면 아래와 같습니다.
5.61 \pm (2.262 \times 0.043) = 5.61 \pm 0.097~ \mathrm{kg}
이것을 말로 표현하면 “이 물체의 질량에 대한 참값은 5.51 kg보다는 크고 5.71 kg보다는 작은 구간내에 있을 확률이 95%이다”라는 것을 의미합니다.




1 thought on “표준 오차 계산 예제”