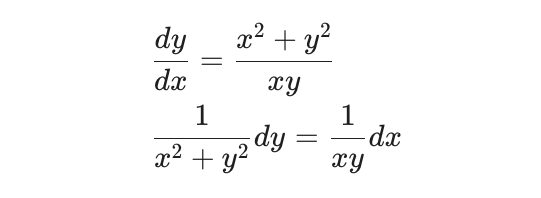Last Updated on 2024-03-18 by BallPen
변수분리가 안되는 미분방정식을 변수분리하여 풀어내는 방법을 알아봅니다.
확장된 변수분리형 미분방정식 풀이 방법을 이번 글에서 소개합니다.
보통의 변수분리형 미분방정식은 변수를 좌변과 우변에 각각 분리한 후 적분을 통해 방정식의 해를 구합니다.
그런데 어떤 미분방정식은 변수분리가 되지 않습니다만 치환을 통해 변수분리가 가능하도록 바꿀 수 있는 것들이 있습니다.
이러한 방식으로 문제를 풀 수 있는 것을 ‘확장된 변수분리형 미분방정식’이라 부릅니다. 또는 ‘변수분리형 미분방정식의 확장된 풀이’라고 부르기도 해요.
아래는 이번 글의 목차입니다.
Contents
1. 변수분리형 미분방정식 복습
아래의 미분방정식은 변수분리가 가능합니다.
\tag{1-1}
y^\prime = f(x)g(y)즉, 다음과 같이 좌변과 우변에 각각의 변수를 분리할 수 있죠.
\tag{1-2}
{{1}\over{g(y)}} dy = f(x)dx양변을 적분하면 비로소 (1-1)식에 주어진 미분방정식의 해를 구할 수 있게 됩니다.
\tag{1-3}
\int{{1}\over{g(y)}} dy = \int f(x)dx이와 같이 변수를 분리한 후 적분하여 해를 구하는 미분방정식을 ‘변수분리형 미분방정식‘이라 합니다.
그런데 어떤 미분방정식은 한번에 변수분리가 되지 않지만, 치환 과정을 거쳐 변수분리가 가능한 형태로 방정식이 변형되는 경우도 있습니다.
이러한 미분방정식을 ‘확장된 변수분리형 미분방정식’이라 부릅니다.
2. 확장된 변수분리형 미분방정식
예를 들어 아래의 미분방정식을 생각해보세요. 도함수 y^{\prime}가 y/x에 의존합니다.
\tag{2-1}
y^\prime = f({{y}\over{x}})이 미분방정식은 좌변과 우변으로 변수 분리가 가능하지 않다고 가정하겠습니다. 그렇지만 y/x를 u로 치환해 볼까요.
\tag{2-2}
y^\prime = f({{y}\over{x}}) = f(u)또한 치환관계로 부터 아래의 식도 성립합니다.
\tag{2-3}
y = xu(2-3)식을 x로 미분하세요.
\tag{2-4}
\begin{align}
y^{\prime} &= {{dx}\over{dx}}u + x {{du}\over{dx}}\\
&=u+x{{du}\over{dx}}
\end{align}그러면 (2-2)식과 (2-4)식은 항등식이 성립합니다.
\tag{2-5}
y^{\prime} = f(u) =u+ x {du \over dx}이렇게 하고 보니 (2-5)식을 자세히 보시면 변수 분리가 가능해 보입니다. 아래와 같이요.
\tag{2-6}
{{1}\over{f(u)-u}}du = {{1}\over{x}}dx변수분리가 가능하니 이제부터는 변수분리형 미분방정식의 풀이 형태로 진행하면 됩니다. 따라서 가장 먼저 (2-6)식의 양변을 적분합니다.
\tag{2-7}
\int{{1}\over{f(u)-u}}du =\int {{1}\over{x}}dx이를 통해 x(u)를 구한 후 u에 y/x를 대입하여 정리하면 (2-1)식의 일반해가 구해진 답니다.
아래의 예제를 풀어보면 더 구체적으로 이해할 수 있어요.
3. 확장된 변수분리형 미분방정식 풀이 예제
3-1. 예제 1
다음의 미분방정식이 주어져 있어요.
\tag{2-1}
\begin{align}
\color{blue} y^{\prime} = {{y}\over{x}} + {{x}\over{y}}\\
\end{align}우선 x,~y의 변수에 대해 좌변과 우변으로 각각 변수분리가 가능한지 검토를 해보면 아래와 같이 변수가 완전히 분리되지 못하는 것을 알 수 있어요.
\tag{2-2}
\begin{align}
&{{dy}\over{dx}} = {{y}\over{x}}+{{x}\over{y}}\\
&{{dy}\over{dx}}={{x^2 + y^2}\over{xy}}\\
&{{1}\over{x^2 + y^2}} dy = {{1}\over{xy}}dx
\end{align}좌변은 y와 관련된 요소들만 모이고, 우변은 x와 관련된 요소들만 모여 있어야 하는데 x와 y가 서로 섞여 있는 것을 알 수 있어요.
그러므로 (2-1)식의 미분방정식은 변수분리형 미분방정식이 아닙니다. 그렇다면 어떻게 하면 문제를 풀 수 있을까요?
위에서 설명드렸듯이 확장된 변수분리형 미분방정식일 수도 있으니 y/x를 u로 치환하겠습니다.
\tag{2-3}
{y \over x} = u\tag{2-4}
y=ux또한 (2-4)식의 양변을 x로 미분하면 다음과 같습니다.
\tag{2-5}
\begin{align}
y^{\prime} = {{dy}\over{dx}} &= {{du}\over{dx}} x + u {{dx}\over{dx}}\\
&={{du}\over{dx}}x + u
\end{align}그리고 u를 이용해 (2-1)식을 다시 표현하면 아래와 같습니다.
\tag{2-6}
y^{\prime} = u + {1 \over u}(2-5)식과 (2-6)식을 같게 놓으면 아래의 식이 성립합니다.
\tag{2-7}
\begin{align}
\cancel u + {1 \over u} = {{du}\over{dx}}x + \cancel u
\end{align}
그런데 (2-7)식을 잘 보면 변수분리가 가능해 보입니다. 원래는 변수분리가 가능하지 않았는데 y/x를 u로 치환하니 변수분리가 가능한 미분방정식이 되었습니다.
그러면 아래와 같이 변수분리를 한 후 통상의 변수분리형 미분방정식을 풀어가는 것과 같은 방식으로 문제를 풀면 됩니다.
\tag{2-8}
u du = {1 \over x} dx(2-8)식의 양변을 적분합니다.
\tag{2-9}
\begin{align}
\int udu &= \int {1 \over x} dx\\
{1 \over 2} u^z + C_1 & = \ln|x| + C_2\\
\ln|x| &= {1 \over 2}u^2 + (C_1 - C_2) \\
\ln|x| &= {1 \over 2}u^2 +C_3\\
\end{align}(2-9)식의 마지막 줄에서 u에 원래의 식인 y/x를 대입합니다.
\tag{2-10}
\begin{align}
\ln{|x|} &= {1 \over 2} \Big({y \over x}\Big)^2 + C_3\\
2 \ln{x} - C_3 &= \Big({{y}\over{x}} \Big)^2\\
\end{align}(2-10)식을 정리하면 다음의 일반해를 구할 수 있습니다. 이때 -C_3는 어차피 상수 -1과 상수 C_3의 곱으로 주어지는 또 다른 상수일 뿐이므로 C로 두었습니다.
\tag{2-11}
\begin{align}
y^2 = 2x^2 \ln x + Cx^2\\
y = \big(2x^2 \ln x + Cx^2\big)^{1/2}
\end{align}(2-11)식을 (2-1)식의 미분방정식에 대입하면 좌변과 우변의 항등관계가 만족되는 것을 알 수 있습니다.
즉, ‘해’라는 뜻이죠.
3-2. 예제 2
다음의 미분방정식을 풀어 보겠습니다.
\tag{2-12}
\color{blue} x y^{\prime} = 2 \sqrt{xy} + y좌변과 우변으로 변수분리가 가능한지 식을 변형해 보세요.
\tag{2-13}
{{dy}\over{dx}} = {{2 \sqrt{xy}+y}\over{x}}\tag{2-14}
{{1}\over{2 \sqrt{xy} + y}}dy = {{1}\over{x}}dx
좌변에는 y와 관련된 것만, 우변에는 x와 관련된 것만 모이면 편한데, 그렇지가 않습니다. 즉 변수분리가 되지 않습니다.
따라서 (2-12)식은 변수분리형 미분방정식이 아닙니다. 그렇지만 혹시 모르니 y/x를 u로 치환해 보겠습니다.
\tag{2-15}
{{y}\over{x}} = u\tag{2-16}
y=ux(2-16)식의 양변을 x로 미분해 보세요.
\tag{2-17}
\begin{align}
y^{\prime} = {{dy}\over{dx}} &= {{du}\over{dx}} x + u {{dx}\over{dx}}\\
&={{du}\over{dx}}x + u
\end{align}한편 (2-12)식을 u를 이용해 정리하면 다음과 같습니다.
\tag{2-18}
\begin{align}
y^{\prime} = {{dy}\over{dx}} &= {{2 \sqrt{xy}+y}\over{x}}\\
&={{2 \sqrt{\cancel{x}y}}\over{\cancel{\sqrt{x}} \sqrt{x}}} + {{y}\over{x}}\\
&={{2\sqrt{y}}\over{\sqrt{x}}} + {{y}\over{x}}\\
&=2\sqrt{{{y}\over{x}}} + {{y}\over{x}}\\
&=2 \sqrt{u} + u
\end{align}그러면 (2-17)식과 (2-18)식은 서로 같아요.
\tag{2-19}
\begin{align}
2 \sqrt{u} + \cancel{u} = {{du}\over{dx}}x + \cancel{u}
\end{align}(2-19)식을 잘 보면 변수분리가 가능해 보입니다. 바로 아래와 같이요.
\tag{2-20}
{{1}\over{x}}dx = {1 \over{2 \sqrt{u}}} du이제부터는 변수분리형 미분방정식의 풀이대로 진행하면 됩니다. 양변을 적분하세요.
\tag{2-21}
\begin{align}
\int{{1}\over{x}}dx &= \int {1 \over{2 \sqrt{u}}} du\\
\ln |x| + C_1 &= {1 \over 2} \big( 2u^{1/2} + C_2 \big)\\
\ln|x| &= \sqrt{u} + \big({1 \over2}C_2 - C_1 \big)\\
\ln|x| &= \sqrt{u} + C
\end{align}(2-21)식의 마지막 줄에 u대신 y/x를 대입하세요. 그러면 아래와 같이 정리하여 일반해를 구할 수 있습니다.
\tag{2-22}
\begin{align}
\ln|x| &= \sqrt{{y}\over{x}} + C\\
\ln{x} &={{\sqrt{y}}\over{\sqrt{x}}} + C\\
\sqrt{y} & = \sqrt{x} \ln|x| + C\sqrt{x}\\
y &= \Big[ \sqrt{x} \ln|x| + C\sqrt{x} \Big]^{-1/2}
\end{align}한편 윗식에서 두번째 줄에서 세번째 줄로 넘어가며 상수 C앞에 마이너스 부호가 붙어야 하지만 붙이지 않았어요. 그 이유는 +C이든 -C이든 어차피 상수 C이기 때문입니다.
3. 확장된 변수분리형 미분방정식 풀이 방법 요약
첫째, 주어진 미분방정식이 변수분리가 되지 않는다면 y/x를 u로 치환해 본다.
둘째, 치환된 미분방정식이 변수분리가 가능한지 검토한다. 변수분리가 가능하다면 변수분리를 한 후 양변을 적분한다.
셋째, 적분으로 해를 구한 후 u에 y/x를 대입하고 정리하여 일반해를 구한다.
넷째, 만일 초기조건이 있다면 이를 활용하여 특수해도 구한다.