베르누이 방정식 그리고 토리첼리 정리

BallPen · 2022-09-03T12:36:44+09:00

베르누이 방정식(Bernoulli's equation)은 일-에너지 정리에 따라 유체에 해준 일이 유체의 역학적 에너지 변화와 같다는 것을 의미합니다. 이 방정식으로 물통에서 구멍을 통해 분출되는 유체의 유출속도를 구하는 토리첼리 정리를 유도할 수 있어요.

Last Updated on 2022-09-03 by BallPen

베르누이 방정식으로부터 토리첼리 정리를 유도해 보겠습니다.

베르누이 방정식 (Bernoulli’s equation)이란 일-에너지 정리에 따라 유체에 해준 일이 유체의 역학적 에너지 변화와 같음을 의미합니다.

또한 토리첼리 정리 (Torricelli’s theorem)란 유체가 들어 있는 통에 구멍이 있을 때 그 구멍을 통해 빠져나오는 유체의 속력을 구하는 공식을 말해요.

베르누이 방정식으로 토리첼리 정리를 이해할 수 있어요. 또한 조금만 더 고민하면 통에서 유체가 모두 빠져나오는데 걸리는 시간도 구할 수 있고요. 시간의 함수로서 통에 남아있는 유체의 높이 변화에 대한 공식도 유도할 수 있답니다.

함께 알아봐요. 아래는 이번 글의 목차입니다.

Contents [hide]

1. 베르누이 방정식 유도
2. 토리첼리 정리

1. 베르누이 방정식 유도

베르누이 방정식 또는 베르누이 정리(Bernoulli’s theorem)란 점성이나 압축특성이 없는 유체가 흐를 때 성립하는 일-에너지 정리를 말합니다.

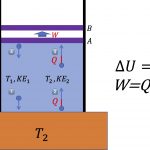
아래 [그림 1]은 관의 한 끝에서 유체가 유입되고 이로 인해 다른 쪽 끝에서 유체가 유출되는 상황을 묘사한 그림입니다. 이때 유체가 압축되지 않는 경우를 가정하므로 연속방정식에 따라 $\Delta t$ 동안 유체의 유입 질량과 유출 질량은 서로 같습니다.

유체가 유입되는 쪽에서 압력 $P_1$ 이 한 일 $W_1$ 은 다음과 같습니다. 이때 유입되는 관의 단면적은 $A_1$ 으로 두겠습니다. 또한 압력에 대한 정의에 따라 $F=PA$ 의 관계를 활용합니다.

\tag{1} W_1 = F_1 \Delta x_1 = P_1 A_1 \Delta x_1 = P_1 V_1

또한 유체가 유출되는 쪽에서 압력 $P_2$ 가 한 일 $W_2$ 는 다음과 같습니다.

\tag{2} W_2 = -F_2 \Delta x_2 = -P_2 A_2 \Delta x_2 = -P_2 V_2

(2)식에서 음의 부호가 붙는 이유는 $F_2$ 의 방향과 $\Delta x_2$ 의 방향이 서로 반대이기 때문입니다.

그렇다면 $\Delta t$ 동안 유체에 한 일짜 일은 다음과 같습니다.

\tag{3} W=W_1 + W_2 = P_1 V_1 -P_2 V_2 = P_1 V - P_2 V

여기서 $V_1$ 과 $V_2$ 를 $V$ 로 바꾼 이유는 비압축성 유체이므로 $V_1$ 과 $V_2$ 가 서로 같기 때문입니다.

(3)식으로 구한 유체에 해준 알짜 일 $W$ 는 유체의 운동에너지 $KE$ 와 위치에너지 $PE$ 를 변화시키는데 사용됩니다. 따라서 다음의 일-에너지 정리가 성립해요.

\tag{4} W=\Delta KE + \Delta PE

이를 구체적으로 풀어쓰면 다음과 같습니다.

\tag{5} P_1 V - P_2 V = \big( {1 \over 2} mv_2 ^2 - {1 \over 2} mv_1^2 \big) + \big( mgy_2 - mgy_1 \big)

양변을 $V$ 로 나눈 후, 밀도 $\rho = m/V$ 의 관계를 이용해서 정리하면 다음과 같습니다.

\tag{6} \color{blue} P_1 + {1 \over 2} \rho v_1^2 + \rho gy_1 = P_2 + {1 \over 2} \rho v_2^2 + \rho gy_2

바로 위에 도출된 (6)식을 ‘베르누이 방정식’이라 부릅니다.

2. 토리첼리 정리

아래 [그림 2]는 물이 들어 있는 물통에 구멍이 있고 그 구멍으로 물이 분출하는 모습을 보여줍니다. 이때 분출되는 물의 속도를 구할 수가 있는데요.

바로 베르누이 방정식으로부터 유도할 수 있으며 최종적으로 도출된 공식을 ‘토리첼리 정리’라고 부릅니다.

[그림 2] 토리첼리 정리는 유체가 들어 있는 통에 구멍이 나 있고 그 구멍으로 분출되는 유체의 속도를 구하는 관계식을 말합니다.(사진인용 https://pxhere.com/)

이제부터 토리첼리 정리를 유도해 보겠습니다.

2-1. 토리첼리 정리 유도

[그림 3]은 단면적이 $B$ 인 물통이 있고 그 물통의 수면으로부터 $h$ 만큼 낮은 곳에 단면적이 $A$ 인 구멍이 뚫려 있어요.

[그림 3] 물이 들어 있는 통에 구멍이 뚫려 있어요. 토리첼리 정리를 이용하면 이 구멍을 통해 빠져나오는 물의 속력을 구할 수 있어요.

이때 큰 물통의 단면적 $B$ 보다 구멍의 단면적 $A$ 는 무척 작다고 가정하겠습니다. 그러면 물이 구멍을 통해 속도 $v_1$ 으로 빠져나온다고 했을 때, 큰 물통의 수면 하강속도 $v_2$ 는 그림과 같이 거의 0으로 간주할 수 있어요.

그 이유는 위에서 말씀 드린 것처럼 물통의 크기가 아주 크다고 가정했기 때문이에요. 커다란 댐에 아주 작은 구멍이 뚫려 있다고 생각하시면 쉽습니다.

그러면 구멍을 통해 분출해 나오는 물의 속력 $v_1$ 을 구해 봐요. 우선 (6)식의 베르누이 방정식을 적용하면 됩니다.

\tag{7} \begin{align} P_1 + {1 \over 2} \rho v_1^2 + \rho g y_1 &= P_2 + {1 \over 2} \rho v_2^2 + \rho gy_2\\ {1 \over 2} \rho v_1 ^2 &= (P_2 - P_1) + {1 \over 2} \rho v_2^2 + \rho g (y_2 - y_1) \\ &=\Delta P + {1 \over 2} \rho v_2^2 + \rho g h \end{align}

이때 [그림 3]처럼 $v_2 \approx 0$ 로 간주하면 (7)식은 다음과 같이 근사할 수 있습니다.

\tag{8} \begin{align} \rho v_1 ^2 = 2(\Delta P + \rho gh)\\ \end{align}

\tag{9} v_1 = \sqrt{2 \over \rho} \sqrt{\Delta P + \rho gh}

마지막으로 $P_1$ 과 $P_2$ 가 대기압으로 서로 같다면 (9)식에서 $\Delta P$ 는 0이 됩니다.

\tag{10} \color{blue}v_1 = \sqrt{2gh}

(10)식을 ‘토리첼리 정리’라고 부릅니다. 이 식이 재미있는 것은 분출되는 물의 속도가 높이 $h$ 에서 자유낙하하는 물체가 지면에 도달할 때 갖는 속도와 공식이 동일하다는 것입니다.

2-2. 물이 모두 빠져나가는데 걸리는 시간

물통에 들어 있는 물은 구멍을 통해 결국 어느 시간이 지나면 모두 빠져나가게 됩니다. 구멍의 높이까지 물이 모두 빠져나가는데 걸리는 시간을 구해볼까요.

시간 $\Delta t$ 동안 [그림 3]에서 단면적이 $A$ 인 구멍을 통해 빠져나간 물의 부피는 다음과 같습니다.

\tag{11} \Delta V = A \Delta x =A v_1 \Delta t

여기서 $\Delta x$ 는 속도 $v_1$ 으로 $\Delta t$ 동안 빠져나온 물의 길이를 뜻합니다.

한편, (11)식으로 주어진 빠져나온 물의 부피는 물통에서 감소하는 물의 부피와 동일할 거에요. 그러므로 다음의 관계가 성립합니다.

\tag{12} \Delta V = -B \Delta h = A v_1 \Delta t

여기서 $B$ 는 물통의 단면적이고, $\Delta h$ 는 물통의 수위 변화량을 뜻합니다. 이때 음의 부호가 붙은 이유는 물이 구멍으로 빠져나갈 수록 물통의 수위는 감소하게 되므로 나중 수위에서 처음 수위를 뺀 $\Delta h$ 가 음수가 되기 때문이에요.

자 이제 평균시간이 아닌 아주 짧은 시간 $dt$ 를 생각하면 (12)식은 다음 (13)식과 같이 표현될 수 있어요. 이때 $v_1$ 에 (10)식의 토리첼리 정리를 그대로 대입합니다.

\tag{13} \begin{align} -Bdh &= A v_1 dt\\ &=A \sqrt{2gh} dt \end{align}

(13)식에서 변수를 각각 분리한 후 양변을 적분합니다. 적분 구간은 [그림 3]을 참고하면 수면의 높이 $y_2$ 에서 처음 시간 0으로 두고 $y_1$ 에서 나중 시간 $T$ 로 두겠습니다.

\tag{14} \begin{align} -\int_{y_2}^{y_1}B {1 \over \sqrt{h}} dh &= \int_{0}^{T} A \sqrt{2g} dt\\ -B\int_{y_2}^{y_1} h^{-1/2} dh &=A \sqrt{2g} \int_{0}^{T} dt\\ -B \Big[ 2 \sqrt{h} \Big]_{y_2}^{y_1} &= A\sqrt{2g} \Big[t \Big]_0^{T} \end{align}

[그림 3]에서 만일 $y_1$ 을 0으로 처리하면 $y_2$ 는 $h$ 가 됩니다. 이때 물통에 있는 최초 수면 높이라는 의미에서 $h$ 를 $H$ 로 바꿀 수 있을거에요. 결국 (14)식의 가장 마지막 줄은 다음과 같이 바꿀 수 있어요.

\tag{15} \begin{align} -B \Big[ 2 \sqrt{h} \Big]_{H}^{0} &= A\sqrt{2g} \Big[t \Big]_0^{T} \\ 0+ 2B\sqrt{H} &= A\sqrt{2g}T \end{align}

(15)식의 두번째 줄을 $T$ 에 대해 정리하면 물이 모두 유출되는데 걸리는 시간 $T$ 를 구할 수 있습니다.

\tag{16} \color{blue}T= {B \over A} \sqrt{2H \over g}

2-3. 시간에 따른 물통 수면의 높이 변화

물통에 있는 구멍을 통해 물이 빠져나가면 시간이 지날수록 물통에 남아있는 물의 수면이 점점 낮아질 거에요. 이번에는 그 물통의 수면 변화를 시간의 함수로서 표현되는 식을 유도해 보겠습니다.

(14)식을 일부 수정하면 되는데요. (14)식의 가장 위쪽 수식을 다시 쓰면 아래와 같습니다.

\tag{17} -\int_{y_2}^{y_1}B {1 \over \sqrt{h}} dh = \int_{0}^{T} A \sqrt{2g} dt

적분 구간을 바꾸어 볼게요. (17)식의 왼쪽 항의 적분 구간에서 $y_2$ 를 최초 높이 $H$ 로 바꾸고 $y_1$ 을 임의의 수면 높이 $h$ 로 바꿉니다.

또한 시간에 대한 적분 구간도 0에서 $t$ 로 바꾸어 줍니다.

\tag{18} -\int_{H}^{h}B {1 \over \sqrt{h}} dh = \int_{0}^{t} A \sqrt{2g} dt

(18)식을 풀면 (14)식의 가장 마지막 줄과 동일한 형태의 수식이 얻어집니다. 다만 적분구간은 다르겠죠.

\tag{19} \begin{align} -B \Big[ 2 \sqrt{h} \Big]_{H}^{h} &= A\sqrt{2g} \Big[t \Big]_0^{t} \\ -2B\sqrt{h} + 2B\sqrt{H} &= A\sqrt{2g}t \end{align}

(19)식을 $\sqrt{h}$ 에 대해 정리합니다.

\tag{20} \sqrt{h} = \sqrt{H} - {A \over{2B}} \sqrt{2g} t

한편 (16)식을 (20)식의 $A$ 에 대입하면 아래와 같습니다.

\tag{21} \begin{align} \sqrt{h} &= \sqrt{H}-{1 \over {2B}} \Big({B \over T} \sqrt{{2H} \over{g}} \Big)\sqrt{2g}t\\ &=\sqrt{H}-{{\sqrt{H}}\over{T}} t\\ &=\sqrt{H} \Big(1-{t \over T} \Big)\\ \end{align}

마지막으로 양변을 제곱해주면 최종적으로 다음의 식을 얻을 수 있습니다.

\tag{22} \color{blue}h=H \Big( 1- {t \over T}\Big)^2

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 6 Average: 4]