Last Updated on 2025-10-18 by BallPen
전위란 무엇이고 전위차와 어떻게 다른지 구분해봐요.
전위(voltage, electric potential)는 전압이라고도 불리는데요. 전기장 내의 한 점에서 전하 q가 갖는 단위 전하 당 위치에너지의 크기 {PE \over q}를 뜻합니다.
따라서 전위 V가 높다면 동일한 거리에서 운동에너지로 변환시 더 빠른 속도로 움직일 수 있어요.
그리고 두 전위의 차이를 전위차(electric potential difference, 또는 전압차)라고 불러요. 전위차 V_{ab}는 단위 전하가 갖는 위치에너지의 차이 {{PE_a}\over{q}}-{{PE_b}\over{q}}이므로 단위 전하에 한 일 {{W}\over{q}}와 그 크기가 같습니다. 이러한 관계를 식으로 표현하면 다음과 같아요.
\begin{align*}
& {W \over q} = {PE_a \over q} - {PE_b \over q}\\[15pt]
&V_{ab} = V_a - V_b
\end{align*}이에 대해 더 구체적으로 알아봐요. 아래는 이번 글의 목차입니다.
이 글에서 사용된 그림파일이 필요한 분은 아래 링크에서 다운받으세요. 맥의 키노트로 작성되었습니다.
맥 키노트 파일 : Voltage.key
1. 균일한 전기장에서의 전위
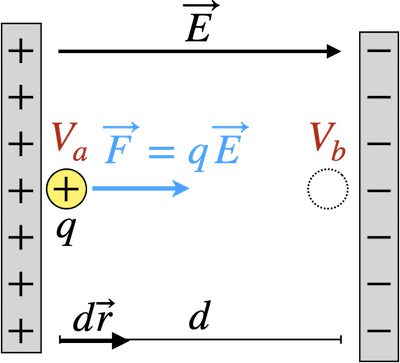
아래 [그림 1]은 양전하와 음전하로 대전된 두 평행판 사이에 균일한 전기장 \vec E가 생성된 모습이에요.
그리고 전하량 q인 양전하가 a지점에 정지상태로 놓여지면 일정한 전기력 \vec F를 받아 d만큼 떨어진 b지점을 향해 가속될거에요.
![[그림 1] 균일한 전기장 내에서 <span class="katex-eq" data-katex-display="false">a</span>점에 놓여진 시험전하는 위치에너지를 갖습니다.](https://ballpen.blog/wp-content/uploads/2024/11/균일한-전기장.jpg)
마치 높은 곳에서 물체를 정지상태로 놓으면 가속되며 떨어지는 상황과 동일합니다. 이때 물체가 떨어지면서 감소한 위치에너지의 크기는 중력을 거슬러 물체를 높은 곳까지 이동시키는데 한 일의 크기와 같습니다.
이 원리를 [그림 1]에 그대로 적용해봐요.
그러면 a지점의 위치에너지 PE_a와 b지점의 위치에너지 PE_b의 차이는 양전하 q를 전기력을 거슬러 b에서 a까지 d만큼 이동시키기 위해 한 일 W와 같아요.
물론 W=Fd=qEd의 관계가 성립하죠.
이를 식으로 정리하면 다음과 같습니다.
\tag{1-1}
\begin{align}
PE_a - PE_b = W=Fd = qEd
\end{align}그런데 윗 식을 보면 전하를 옮기는데 한 일 W의 크기가 시험전하의 전하량 q에 의존하는 것을 알 수 있어요. 즉 q가 커지면 W도 커지게 되는 것이죠.
따라서 단위전하당 일로 규격화하기 위해서는 (1-1)식의 양변을 q로 나눠주면 될거에요. 그러면 아래와 같습니다.
\tag{1-2}
{{PE_a} \over q} - {{PE_b}\over q} = Ed1-1. 전위와 전위차
이제 {{PE_a}\over{q}}를 a점에서의 전위 V_a로, {{PE_b}\over{q}}를 b점에서의 전위 V_b로 치환해서 표기해봐요.
\tag{1-3}
V_a - V_b =Ed그런데 여기서 하나만 더 깊이 생각해 볼게요.
뭐냐면, 변화량에 관한 이야기인데요. 과학에서는 변화량을 구할 때 항상 나중값에서 처음값을 뺍니다. 또는 측정값에서 기준값을 빼죠. 하고 싶은 말은 변화량을 구하기 위해서는 항상 기준이 있어야 하고, 그래야 나중값 또는 측정값에서 빼줄 수 있다는 거에요.
(1-3)식 좌변에도 두 전위의 차이, 즉 전위차(전위의 변화량)가 나오는데요. 둘 중 무엇이 기준점에서의 전위인지를 알아야 변화량을 정확히 표현할 수 있어요.
그렇다면 기준점을 정해야 하는데요.
[그림 1]에서 전기력선이 a점에서 b점을 향합니다. 이를 참조해서 a점의 전위를 기준점으로 한다면 b점의 전위는 관심점에서의 전위가 될거에요.
따라서 a점 전위를 기준으로 b점 전위와의 차이를 구하고 싶다면 (1-3)식의 좌변은 V_a - V_b가 아닌 V_b - V_a로 표기해야 올바른 표현이 됩니다.
결국 이를 반영하면 (1-3)식은 다음과 같이 바뀌어야 해요.
\tag{1-4}
V_b - V_a = - Ed한편 윗식의 우변이 -Ed가 도출되도록 벡터로 표현하면 전기장 \vec E와 미소변위 d \vec r를 스칼라 곱하고 기준점인 a=0에서부터 관심점인 b=d까지 적분해주면 된다는 것을 알 수 있어요.
전위차 V_{ba}를 도입하여 (1-4)식을 일반화하면 다음과 같아요.
\tag{1-5}
V_{ba} = V_b - {\color{blue}V_a} = -\int_{{\color{blue}a=0}}^{b=d} \vec E \cdot d \vec r기억하세요. 항상 기준점에서의 값들이 위 식의 파랑색 부분에 대입되어야 한다는 것을요. 이것이 헷갈리면 올바른 전위차를 구할 수 없어요.
그렇다면 만일 b점 전위 대비 a점 전위와의 차를 구하고 싶다면 어떻게 해야 할까요? 즉 V_a - V_b를 구하고 싶다면 (1-5)식은 다음과 같이 바뀝니다.
\tag{1-6}
V_{ab} = V_a - V_b = -\int_{b=d}^{a=0} \vec E \cdot d \vec r기준점이 b로 바뀌었으므로 적분구간의 하한도 b에 대한 것으로 바뀌어야 함을 알 수 있어요.
1-2. 예제
[그림 1]에서 V_b를 0~\rm V로 간주하고, 두 평행판 사이의 전기장이 E= 20 ~\rm {N/C}이라고 해봐요. 그리고 평행판 사이의 떨어진 거리는 0.5~\rm cm입니다. a점에서의 전위 V_{a}를 구해보세요.
(Sol) 이 문제는 (1-5)식 또는 (1-6)식을 적용하면 됩니다. 어떤 식을 적용하던 같은 결과가 얻어지겠죠.
먼저 (1-5)식을 적용해봐요.
\tag{1-7}
\begin{aligned}
0- V(a) &= -\int_0^d \vec E \cdot d \vec r\\[8pt]
&=-\int_0^d E dr\\[8pt]
&=-E \int_0^d dr\\[8pt]
&=-E\Big[r\Big]_0^d\\[8pt]
&=-Ed\\[8pt]
&=-(20~\rm {V/m}) \times (0.5\times10^{-2}~\rm m)\\[8pt]
&=-0.1~\rm{V}
\end{aligned}결국 V_a는 다음과 같습니다.
\begin{align*}
V(a) = 0.1~\rm V
\end{align*}이번에는 (1-5)식을 적용해봐요.
\tag{1-8}
\begin{aligned}
V_a - 0 &= -\int_{d}^{0} \vec E \cdot d \vec r\\[8pt]
&=-\int_d^0 Edr\\[8pt]
&=-E\Big[r\Big]_d^0\\[8pt]
&=-\Big((E\times0)-(Ed)\Big)\\[8pt]
&=Ed\\[8pt]
&=0.1~\rm V
\end{aligned}같은 결과가 나왔음을 알 수 있습니다.
2. 불균일한 전기장에서의 전위
2-1. 전위와 전위차
이번에는 전기장이 균일하지 않은 경우의 전위와 전위차를 알아봐요.
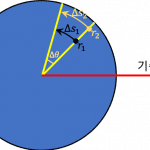
![[그림 2] 불균일한 전기장 내에서 <span class="katex-eq" data-katex-display="false">a</span>점에 있는 시험전하는 위치에너지를 갖습니다.](https://ballpen.blog/wp-content/uploads/2024/11/불균일한-전기장-1-1024x1024.jpg)
대전된 평행판 사이의 일정한 전기장과 달리 [그림 2]의 점전하에 의한 전기장의 크기는 아래 식과 같이 거리에 따라 달라지게 됩니다.
\tag{2-1}
\vec E = k{Q \over r^2} \hat r그런데 시험전하는 a점에서 단위전하당 위치에너지를 갖는데요. 이 시험전하가 b점으로 이동하면 두 지점 사이의 단위전하당 위치에너지의 차이가 존재합니다. 그것이 전위차이죠.
이때 전기력선이 시작되는 a점의 전위를 기준전위로, 전기력선이 끝나는 b점의 전위를 관심점의 전위로 한다면 전위차 식은 다음과 같습니다.
\tag{2-2}
V_{ba} = V_b - V_a = -\int_{r_a}^{r_b} \vec E \cdot d \vec r그럼 (2-1)식을 (2-2)식에 대입해서 정리해 볼께요.
\tag{2-3}
\begin{aligned}
V_{ba} = V_b - V_a &= - \int_{r_a}^{r_b} k{Q\over r^2} \hat r \cdot d \hat r\\[8pt]
&=-kQ\int_{r_a}^{r_b}{1 \over r^2} dr\\[8pt]
&=-kQ\Big[-{1 \over r}\Big]_{r_a}^{r_b}\\[8pt]
&=k{Q \over r_b} - k{Q \over r_a}
\end{aligned}윗 식이 바로 점전하에 의한 전위차를 나타내는 공식입니다.
만일 무한대의 전위를 기준으로 b점 전위와의 차이를 구하고 싶다면 윗 식에서 기준점인 r_a를 무한대로 바꾸면 됩니다. 그러면 분모가 무한대가 되니 V_a =0이 됩니다.
그러면 다음과 같아요.
\tag{2-4}
\begin{aligned}
V_{b} &= k{Q \over r_b} - k{Q \over \infty}\\[8pt]
&=k{Q \over r_b}
\end{aligned}따라서 윗 식과 같이 무한대, 즉 전위가 0인 점을 기준으로 점전하로부터 r만큼 떨어진 곳의 전위는 다음과 같이 구할 수 있습니다.
\tag{2-5}
V = k{Q \over r}2-2. 예제
[그림 2]를 참고하세요. 원천전하의 전하량이 Q={1.11 \times 10^{-10}~\rm C}입니다. 이 원천전하로부터 r_a = 2.00~\rm m점의 전위를 기준으로 r_b = 4.00~\rm m점과의 전위차를 구하세요. 그리고 각 지점의 전위도 구하세요.
(Sol) 이 문제를 풀기 위해서는 (2-5)식을 적용하면 됩니다. 먼저 a점의 전위를 구해 봐요.
\tag{2-6}
\begin{aligned}
V_{a} &= k{Q \over r_a}\\[8pt]
&={(9 \times10^9~\rm{N \cdot m^2/C^2}){(1.11 \times 10^{-10} ~\rm C )}\over{2.00~\rm m}}\\[8pt]
&=0.50~\rm V
\end{aligned}이번에는 b점의 전위입니다.
\tag{2-7}
\begin{aligned}
V_{b} &= k{Q \over r_b}\\[8pt]
&={(9 \times10^9~\rm{N \cdot m^2/C^2}){(1.11 \times 10^{-10} ~\rm C )}\over{4.00~\rm m}}\\[8pt]
&=0.25~\rm V
\end{aligned}그러므로 a점의 전위를 기준으로 했을 때 b점과의 전위차는 다음과 같아요.
\tag{2-8}
\begin{aligned}
V_{ba} &= V_b - V_a\\[3pt]
&=0.25~\rm V - 0.50~\rm V\\[3pt]
&=-0.25~\rm V
\end{aligned} 여기서 V_{ba}가 음수가 나왔는데요. 이것은 V_a에 비해 V_b의 전위가 0.25 V 작다는 의미입니다.
3. 도체에서의 전위
[그림 3]은 바깥과 안쪽 반지름이 각각 a와 b인 도체 껍질 속에 반지름 R인 도체구가 놓여있는 것을 보여주고 있어요.
이때 도체 구가 양전하 q로 대전되어 있다면 도체구 중심에서의 전위를 계산해 봐요. 이때 기준점은 무한대 지점으로 하겠습니다.
![[그림 3] 도체 껍질 속에 있는 도체 구가 <span class="katex-eq" data-katex-display="false">+q</span>로 대전되어 있을 때 도체 구 중심의 전위 값을 구해 보세요](https://ballpen.blog/wp-content/uploads/2024/11/도체에서의-전위-1024x531.jpg)
도체의 성질에 따르면 대전된 도체구의 전하 q는 모두 표면에만 존재합니다.
그래서 도체 구 표면에 전하들이 분포되어 있음을 알 수 있어요. 그리고 이 전하들은 정전기 유도를 일으켜 도체 껍질의 안쪽 표면에 -q의 전하를 유도하고 바깥 껍질에는 q를 유도하게 됩니다.
가우스 법칙을 적용하면 각 영역의 전기장을 구할 수 있는데요. 다음과 같습니다.
\begin{align*}
&E_1 = 0 ~~~~~~~~~~~~~~~~~~~~~~~~도체~구~~안 (r < R) \\[10pt]
&E_2 ={k{q \over r^2}}~~~~~~~~~~~~~~~~~~~~도체~구와~껍질~사이 (R < r < a) \\[10pt]
&E_3 =0~~~~~~~~~~~~~~~~~~~~~~~~도체 ~껍질 ~안 (a< r< b) \\[10pt]
&E_4 =k{q \over r^2}~~~~~~~~~~~~~~~~~~~도체 ~껍질 ~밖 (b < r)
\end{align*}전기장을 구했으니 이제 (2-2)식을 적용하면 도체 구 중심에서의 전위 V를 구할 수 있어요. 아래 수식에서 빨강색 전기장은 모두 0이에요
\tag{3-1}
\begin{aligned}
V &= -\int_{\infty}^{0} \vec E \cdot d \vec r\\[10pt]
&=\Big(-\int_{R}^{0} {\color {red}E_1} dr \Big) +\Big(- \int_a^R E_2 dr \Big)+\Big( - \int_{b}^{a}{\color{red}E_3}dr \Big) + \Big(-\int_{\infty}^{b}E_4dr\Big)\\[10pt]
&=\Big( - \int_a^R \big ({k {q \over r^2}}\big)dr\Big) + \Big(-\int_{\infty}^b \big ({k {q \over r^2}}\big)dr\Big)\\[10pt]
&=\Big[{{kq}\over{r}}\Big]_a^{R} + \Big[{{kq}\over{r}}\Big]_{\infty}^b\\[10pt]
&={k{{q}\over{R}}} - {k{{q}\over{a}}} + {k{{q}\over{b}}}+{k{{q}\over{\infty}}}\\[10pt]
&={k{{q}\over{R}}} + {k{{-q}\over{a}}} + {k{{q}\over{b}}}
\end{aligned}윗 식의 결과를 보시면 마치 R만큼 떨어진 곳에 양전하 q가, a만큼 떨어진 곳에 음전하 -q가, b만큼 떨어진 곳에 양전하 q가 있을 때 원점에서의 전체 전위를 구하는 것과 같다는 것을 알 수 있어요.