반감기(half-life) 뜻과 공식 유도

BallPen · 2022-12-02T09:25:48+09:00

반감기(half-life)는 방사성원소가 붕괴되어 부모핵 갯수가 절반으로 줄어드는데 걸리는 시간을 말합니다. 방사성원소는 붕괴 법칙에 따라 자연적으로 부모핵이 자녀핵으로 변환됩니다. 반감기를 이해하기 위해 붕괴곡선을 해석하고 반감기 공식도 유도합니다.

Last Updated on 2022-12-02 by BallPen

핵물리학에서 자주 등장하는 반감기 개념에 대해 알아봅니다.

반감기(half-life)는 방사성 원소의 양이 현재의 절반으로 줄어드는 데 걸리는 시간을 말합니다.

반감기는 연대 측정 분야에서 많이 사용되는데요. 이번 글에서는 그 반감기에 대해 함께 알아봐요.

아래는 이번 글의 목차입니다.

Contents

1. 방사성 원소의 붕괴
2. 방사성 원소의 붕괴율
- 3-1. 붕괴의 법칙 (시간에 따른 부모핵의 갯수 변화)
- 3-2. 붕괴의 활성도 (붕괴율, 방사능세기)
4. 반감기
- 4-1. 붕괴곡선을 통한 반감기 이해
- 4-2. 반감기 공식 유도

1. 방사성 원소의 붕괴

반감기를 이해하기 위해서는 우선 방사성 원소(radioactivity element)가 무엇이고, 그것이 붕괴 된다는 것이 무슨 의미인지를 알아야 합니다.

방사성 원소는 방사선(radiation)을 방출하는 원소를 말합니다. 또한 방사선을 방출하는 성질을 방사능(radioactivity)이라고 부르죠.

그러면 방사선은 무엇일까요?

방사성 원소는 안정된 상태가 아닙니다. 이 말은 충분한 시간이 지나면 한 원소(부모핵)에서 다른 원소(자녀핵)로 변하게 되는데요. 이것을 방사성 원소가 붕괴된다고 말합니다.

그리고 붕괴 과정에서 헬륨원자핵인 $\alpha$ 선, 전자선인 $\beta$ 선, 전자기파인 $\gamma$ 선이 원소의 핵으로부터 방출되는데요, 이것이 방사선이에요.

예를 들면 아래에 방사성 원소의 붕괴식이 있어요.

\tag{1} {^{238}_{92}\mathrm{U}} ~\rightarrow ~{^{234}_{90}\mathrm{Th}~ +~ ^{4} _{2} \mathrm{He}}

\tag{2} {^{14}_{6}\mathrm{C}} ~\rightarrow ~{^{14}_{7}\mathrm{N}~ +~ e^{-} ~+~\bar{\nu}}

(1)식에서 $^{238}_{92}\mathrm{U}$ 은 $\mathrm{U}$ 의 원소 기호를 갖는 방사성 원소인 우라늄을 뜻합니다. 앞에 있는 숫자 중 92와 238은 원자번호(atomic number)와 질량수(mass number, 핵자수라고도 불림)입니다

여기서 원자번호는 우라늄 원자핵에 있는 양성자의 갯수입니다. 아울러 질량수는 양성자와 중성자 갯수의 합을 뜻해요. 따라서 $^{238}_{92}\mathrm{U}$ 는 양성자가 92개 있고 양성자와 중성자의 합이 총 238개 있다는 의미입니다. 즉 중성자는 238개에서 92개를 뺀 146개가 존재합니다.

우라늄은 방사성 원소이기 때문에 불안정해요. 그러므로 충분한 시간이 지나면 결국 붕괴되어 다른 원소로 바뀌게 됩니다.

이 말은 붕괴전인 부모핵과 붕괴후인 자녀핵이 주기율표에서 서로 다른 자리를 차지한다는 말입니다.

[그림 1] 주기율표. 방사성 붕괴가 일어나면 원소의 종류가 달라집니다. 즉 방사성 붕괴전의 부모핵과 붕괴후의 자녀핵의 원소는 서로 달라요. 즉 (1)식에서 부모핵인 92번 우라늄과 90번 자녀핵인 토륨은 주기율표에서 서로 다른 자리를 차지하는 서로 다른 원소입니다. (그림 인용: wikimedia)

(1)식을 보면 부모핵인 우라늄이 자녀핵인 토륨으로 바뀌는데요, 이때 토륨의 양성자 수는 90개이고, 양성자와 중성자의 총 합은 234개가 됩니다. 그리고 붕괴과정에서 양성자 2개와 질량수가 총 4개인 헬륨원자 핵 $^4_2 \mathrm{He}$ 을 방출하게 됩니다.

바로 이 헬륨 원자핵이 $\alpha$ 선이에요.

(2)식에서는 탄소원자가 부모핵이 되고 질소원자가 자녀핵이 됩니다. 이 붕괴과정에서 중성자가 양성자로 변하면서 반중성미자와 함께 전자 $e^{-}$ 를 방출합니다. 바로 이 전자가 $\beta$ 선이에요. 참고로 $e^{+}$ 인 양전자도 있을 수 있어요. 이것도 $\beta$ 선에 포함됩니다.

이와 유사하게 어떤 방사성 물질은 붕괴과정에서 광자를 방출하는데 그때 방출되는 광자가 $\gamma$ 선이 되는거에요.

2. 방사성 원소의 붕괴율

방사성 원소가 $\alpha$ 선, $\beta$ 선, $\gamma$ 선을 방출하며 붕괴되면 부모핵이 자녀핵으로 바뀌게 된다고 위에서 말씀드렸어요.

간혹 원자의 핵이 바뀌는 붕괴 과정과 핵 주변을 도는 전자의 갯수가 변하는 이온화 과정을 헷갈려하는 분들이 있어요.

붕괴과정은 원자 핵에서 벌어지는 일이기 때문에 원소의 종류가 변합니다. 쉽게 말해 금이 은으로 바뀌는 개념이에요. 이에 비해 이온화 과정은 원자핵은 변하지 않고 주변에 있는 전자의 갯수만 바뀌기 때문에 원소가 달라지는 것은 아닙니다. 그냥 금은 금일 뿐이에요. 다만 화학적 성질은 달라질 수 있어요.

방사성 원소의 붕괴과정에서 단위시간당 붕괴되는 원소의 비율은 어떻게 될까요? 즉 1초당 몇 개의 부모핵이 자녀핵으로 변하는지에 대한 질문입니다.

이에 대해 많은 연구가 이루어졌어요. 그 결과 다음과 같은 놀라운 결과를 얻게 됩니다.

간단히 말하면, 방사성 원소의 붕괴율은 현재 방사성 원소 부모핵의 갯수에 비례합니다. 이것을 식으로 표현하면 다음과 같아요.

\tag{3} \color{blue}R = - {{dN}\over{dt}} = kN

여기서 $N$ 은 부모핵의 갯수에요. 즉 방사성 원소를 구성하는 원자가 있잖아요. 그 원자의 갯수를 말합니다. 또한 $dN/dt$ 을 붕괴율이라고 불러요. 그리고 붕괴율 앞에 있는 음의 부호는 시간이 흐를수록 $N$ 이 감소한다는 의미를 갖습니다.

그리고 $k$ 는 붕괴상수(decay constant)로서 1/s의 단위를 갖는 물질마다 서로 다른 값입니다. $k$ 값이 큰 물질일수록 더욱 빠른 속도로 붕괴가 일어남을 뜻해요.

한편 붕괴율 $dN/dt$ 앞에 있는 음의 부호를 붕괴상수 $k$ 에 넣는 경우도 있어요. 그 경우에 $k$ 값은 음수가 됩니다.

이 글에서는 (3)식과 같이 $k$ 를 양수로 하고 붕괴율 앞에 음의 부호를 붙이도록 할께요.

방사성 원소와 질량수	붕괴 상수, $k$ (1/s)
우라늄 238	$5.0 \times 10^{-18}$
플루토늄 239	$9.2 \times 10^{-13}$
탄소 14	$3.9 \times 10^{-12}$
라듐 226	$1.35 \times 10^{-11}$
라돈 220	$1.33 \times 10^{-2}$
리튬 8	0.825
비스무스 214	$4.33 \times 10^{3}$

[표 1] 방사성 원소에 따른 붕괴 상수. 붕괴상수가 클수록 더욱 큰 붕괴율을 갖습니다. 이 말은 단위시간당 부모핵이 자녀핵으로 많이 바뀌게 된다는 의미에요.

3-1. 붕괴의 법칙 (시간에 따른 부모핵의 갯수 변화)

(3)식에 주어진 방사성 원소의 붕괴율은 변화율을 포함하고 있어요. 이러한 식을 미분방정식이라고 부릅니다.

(3)식에 주어진 미분방정식은 전형적인 변수분리형 미분방정식이에요. 이 미분방정식의 해를 구하기 위해서는 변수를 좌변과 우변으로 각각 분리한 후에 적분하면 됩니다.

이를 위해 좌변은 $N$ 과 관련된 식으로, 우변은 $t$ 와 관련된 식으로 정리해봐요. 상수 $k$ 는 우변으로 보낼게요.

\tag{4} {{1}\over{N}}dN = - k dt

이제 양변을 적분한 후 $N$ 에 대해 정리해 봐요. 적분 구간은 $t=0$ 일 때 부모핵의 갯수를 $N_0$ , 임의 시간 $t$ 일 때 부모핵의 갯수를 $N$ 으로 설정하겠습니다.

\tag{5} \begin{align} \int^N_{N_0}{1 \over N} dN &= - k \int ^t_0 dt\\ \ln{N} - \ln {N_0} &= - k (t-0)\\ \ln{{N}\over{N_0}} &= - k t \end{align}

위 식에서는 로그의 성질이 적용되었습니다. 마지막 식의 양변에 exponential을 취해봐요.

\tag{6} \begin{align} e^{\ln{N/N_0}} &= e^{-kt}\\ {N \over N_0} &= e^{-kt}\\ \end{align}

그리고 $N$ 에 대해 정리해봐요. 그러면 아래의 식이 얻어집니다.

\tag{7} \begin{align} \color{blue}N & \color{blue}=N_0 e^{-kt} \end{align}

이 식을 붕괴의 법칙(radioactivity decay law)이라고 부릅니다. 만일 방사성 원소의 최초의 양 $N_0$ 와 현재 남은 양 $N$ 을 알면 (7)식을 통해 경과한 시간 $t$ 를 알 수 있습니다.

이러한 성질을 연대측정 분야에서 활용하는 거에요.

3-2. 붕괴의 활성도 (붕괴율, 방사능세기)

이번에는 붕괴의 활성도를 알아보겠습니다. 붕괴의 활성도는 단위시간당 붕괴하는 핵의 갯수의 변화율, 즉 붕괴율과 같은 의미에요.

(3)식을 보면 붕괴율 $dN/dt$ 은 부모핵의 양인 현재 방사성 원소의 원자 갯수 $N$ 에 비례합니다. 그러니까 방사성 원소의 양이 많으면 붕괴율이 크고, 양이 작으면 붕괴율도 작아요.

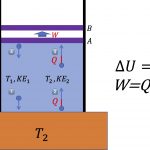
이 개념을 온도로 비유하면 생각하기 쉬울 수 있어요.

예를 들어 다리미를 사용하다 전원을 껏다고 생각해봐요. 그때 다리미의 최초 온도는 120도 였어요. 이때 120도의 뜨거운 다리미는 10초당 5도씩 떨어진다고 했을때 다리미가 식어서 40도가 되면 똑같은 10초당 0.17도씩 떨어지는거에요.

그러니까 현재 온도 $T$ 가 높을 수록 온도변화율 ${\Delta T}/{\Delta t}$ 가 큰것이죠.

따라서 시간이 경과할수록 방사성원소 부모핵의 갯수가 점점 줄어들고, 그에 따라 붕괴율도 작아져요. 이제 그 붕괴율을 시간의 함수로 표현하는 식을 구해볼까요?

우선 (3)식이 저 위에 있으니 다시 한번 더 쓰겠습니다.

\tag{8} \color{blue}R = - {{dN}\over{dt}} = kN

(8)식의 $N$ 에 (7)식을 대입해 봐요.

\tag{9} \begin{align} \color{black}R = - {{dN}\over{dt}} &= kN\\ R = -{{dN}\over{dt}}&=k N_0 e^{-kt} \end{align}

(9)식에서 $kN_0$ 가 무엇인지를 알기 위해 시간 $t$ 에 0을 대입해봐요. 그러면 다음과 같습니다.

\tag{10} \begin{align} R_{t=0} = -{{dN}\over{dt}}&=k N_0 e^{-kt}\\ &=kN_0 e^{-k\times0}\\ &=kN_0 e^{0}\\ &=kN_0 = R_0 \end{align}

(10)식과 같이 $t=0$ 일때 붕괴율은 상수 $kN_0$ 가 되므로 이것을 $R_0$ 로 두도록 하겠습니다.

결국 (9)식의 마지막 줄을 다시 정리하면 다음과 같습니다.

\tag{11} \begin{align} \color{blue}R =R_0 e^{-kt} \end{align}

(11)식의 $R$ 을 붕괴율, 방사능의 세기, 활성도(activity) 등으로 표현합니다. $R$ 의 단위는 Bq라 쓰고 베크렐이라고 읽습니다.

\tag{12} \mathrm{1 Bq = 1붕괴/s}

또한 ‘Ci’로 표기하는 ‘퀴리’라 불리는 단위도 사용할 수도 있어요. ‘베크렐’과 ‘퀴리’ 사이의 단위 환산 인자는 다음과 같아요.

\tag{13} 1~ \mathrm{Ci} = 3.7 \times 10^{10}~ \mathrm{{붕괴/s}} = 3.7 \times 10^{10}~ \mathrm{Bq}

4. 반감기

방사성 원소는 시간을 두고 점점 붕괴되어 다른 원소로 바뀌게 되는데요. 최초 방사성 원소의 양에서 절반만큼 붕괴되는데 걸리는 시간을 반감기라고 합니다. 따라서 반감기는 시간의 단위를 가져요.

4-1. 붕괴곡선을 통한 반감기 이해

아래 [그림 2]는 방사성 원소 부모핵의 갯수가 최초에 100개가 있다고 가정하고, 붕괴상수는 $k=1~(\mathrm{1/s})$ 로 두었을 때 (7)식을 이용해 시간에 따른 부모핵의 갯수 변화를 나타냅니다.

[그림 2] 붕괴곡선과 반감기 <span class="katex-eq" data-katex-display="false">t_{1/2}</span>. 최초 방사성 원소의 부모핵이 100개가 있다고 했을때 50개가 붕괴되고 나머지 50개가 남게 되는 경과시간을 반감기 <span class="katex-eq" data-katex-display="false">t_{1/2}</span>라고 합니다. — [그림 2] 붕괴곡선과 반감기 $t_{1/2}$ . 최초 방사성 원소의 부모핵이 100개가 있다고 했을때 50개가 붕괴되고 나머지 50개가 남게 되는 경과시간을 반감기 $t_{1/2}$ 라고 합니다.

이때 $N_0 = 100$ 개의 절반이 붕괴되어 $N=(1/2)N_0 = 50$ 개의 부모핵만이 남았을때의 경과시간을 반감기 $t_{1/2}$ 라고 합니다.

이 반감기는 현재의 양이 서로 다를지라도 언제든지 똑 같습니다. [그림 2]에서 $(1/2)N_0 = 50$ 개의 절반인 $(1/4)N_0 = 25$ 가 되는데 걸리는 시간 $(2t_{1/2} - t_{1/2})$ 도 반감기 $t_{1/2}$ 로서 동일한 값을 갖게 되요.

정말 신기하죠. 아래는 여러 방사성 원소의 반감기 값입니다.

방사성 원소와 질량수	반감기
우라늄 238	$4.5 \times 10^{9} ~\mathrm{years}$
플루토늄 239	$2.4 \times 10^{4}~ \mathrm{years}$
탄소 14	$5570~ \mathrm{years}$
라듐 226	$1622~ \mathrm{years}$
라돈 220	$52~ \mathrm{s}$
리튬 8	$0.84 ~\mathrm{s}$
비스무스 214	$1.6 \times 10^{-4} ~\mathrm{s}$

[표 2] 여러 방사성 원소의 반감기 값

이제는 반감기를 수식으로 유도해 보겠습니다.

4-2. 반감기 공식 유도

위에서 설명했듯이 반감기란 방사성 원소의 붕괴로 부모핵의 절반이 자녀핵으로 변환되는데 걸리는 시간을 말합니다.

최초 부모핵의 갯수를 $N_0$ 라고 하고, 반감기를 $t_{1/2}$ 라고 했을 때 (7)식에서 $N$ 은 $(1/2)N_0$ 와 같습니다.

반감기 개념을 반영하면 (7)식은 다음과 같이 변형될 수 있어요.

\tag{14} \begin{align} {1 \over 2} \cancel{N_0} &= \cancel{N_0} e^{-kt_{1/2}}\\ {1 \over 2} &= e^{-k t_{1/2}}\\ \end{align}

양변에 자연로그를 적용해 보세요.

\tag{15} \begin{align} \ln {1 \over 2} &= \ln^{e^{-k t_{1/2}}}\\ \ln1 - \ln 2 &= -kt_{1/2}\\ 0 - 0.693 &= -k t_{1/2} \end{align}

결국 (15)식을 $t_{1/2}$ 에 대해 정리하면 다음과 같이 반감기를 구할 수 있습니다.

\tag{16} \begin{align} \color{blue}t_{1/2} = {{0.693}\over{k}} \end{align}

이상으로 이번 글에서는 방사성 원소의 붕괴와 붕괴율, 붕괴의 법칙, 붕괴의 활성도, 반감기 등에 대해 알아봤습니다.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 35 Average: 4.3]

반감기(half-life) 뜻과 공식 유도