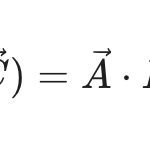Last Updated on 2025-09-30 by BallPen
회로에서 저항기의 역할과 저항기들이 직렬과 병렬연결되었을 때 합성 저항을 어떻게 구하는지 알아봐요.
저항기(resistor)란 저항의 성질을 갖는 전자 부품을 말합니다. 그래서 저항기의 저항이 클 수록 회로에 흐르는 전류는 작아지고, 저항이 작을 수록 전류는 커집니다.
저항기들은 회로에서 직렬 또는 병렬연결될 수 있는데요. 그때 등가 합성 저항 구하는 방법을 알아볼거에요.
결론부터 말씀드리면 저항기 R_1, R_2, R_3가 직렬연결되었거나 병렬연결되면 합성 저항 R_{\rm T}는 다음 식으로 구할 수 있어요.
\begin{align*}
&R_{\rm T} = R_1 + R_2 + R_3 ~~(직렬~연결)\\[10pt]
&{1 \over {R_{\rm T}}} = {1 \over R_1} + {1 \over R_2} + {1 \over R_3}~~(병렬~연결)
\end{align*}이제부터 저항기에 대해 상세히 알아봐요. 아래는 이번 글의 목차입니다.
Contents
글에 사용된 그림파일은 아래에서 다운받을 수 있습니다. 키노트 파일이 원본이고 파워포인트 파일은 변환된 파일이에요. 그래서 파워포인트 파일은 호환성 문제로 그림이 약간 깨져 있을 수 있어요.
맥 키노트 파일: resistors.key
파워포인트 파일: resistors.pptx
1. 저항기와 회로 기호
저항(resistance)은 전류의 흐름을 방해하는 성질이에요. 그리고 저항을 갖도록 만들어진 장치를 저항기(resistor)라고 합니다.
저항기는 일반적으로 아래 [그림 1]과 같이 생겼어요. 모양도 서로 다르고 표면에 여러 줄의 색코드가 있어 이를 판독하면 저항값을 알 수 있어요. 제법 커보이지만 실제로 보면 손톱보다도 작은 것이 대부분이에요.
![[그림 1] 저항기 실물 모습(그림 인용: Windell Oskay)](https://ballpen.blog/wp-content/uploads/2024/06/437342078_2ceeca336e_k-1024x768.jpg)
![[그림 2] 저항기 회로 기호](https://ballpen.blog/wp-content/uploads/2024/06/resistor_symbol.jpg)
[그림 2]는 저항기의 회로기호입니다.
회로도에서 직선은 저항이 없는 도선을 의미해요. 그런데 저항기 기호는 그 도선이 지그재그로 꺽여 있어 전류 흐름을 방해하는 성질이 있음을 의미해요.
사실 모든 도선은 저항이 있어요. 그래서 그 도선 자체가 저항기의 역할을 하게 되는데요.
도선의 길이를 L, 도선의 단면적을 A, 도선의 소재가 갖는 고유한 값인 비저항을 \rho라 할 때 저항 R은 다음과 같이 주어집니다.
\tag{1-1}
R = \rho {L \over A}결국 비저항이 큰 소재를 사용하고, 길이를 길게, 그리고 단면적을 작게하면 저항은 커집니다.
참고로 20^{\circ}{\rm C}에서 몇가지 물질의 비저항은 다음 표와 같아요.
| 물질 | 비저항, \rho( \rm {\Omega \cdot m}) |
|---|---|
| 은 | 1.59 \times 10^{-8} |
| 구리 | 1.68 \times 10^{-8} |
| 금 | 2.44 \times 10^{-8} |
| 알루미늄 | 2.82 \times 10^{-8} |
| 탄소(그래파이트) | (3 \sim 60) \times 10^{-5} |
| 규소 | 20 \sim 2300 |
| 유리 | 10^{10} \sim 10^{14} |
2. 직류전원과 연결된 저항기
아래 [그림 3]은 R=15 ~\Omega의 저항을 갖는 저항기가 10 V의 직류 전원과 연결된 모습을 나타냅니다.
여기서 우리가 알아야 할 개념 두가지가 있는데요.
하나는 저항기에서의 ‘전압강하’이고, 다른 하나는 ‘옴의 법칙’을 적용하여 회로를 통과하는 전류를 구하는 방법을 이해하는 거에요.
하나씩 알아봐요.
![[그림 3] 저항기가 직류 전원과 연결되면 옴의 법칙에 따라 전류가 흐릅니다.](https://ballpen.blog/wp-content/uploads/2024/06/저항회로-1024x568.jpg)
2-1. 전압 강하
[그림 3]을 보면 직류전원의 전압이 10 V라고 되어 있는데요. 이 말은 전원의 양극과 음극의 기전력 차이가 10 V임을 뜻해요.그래서 양극을 10 V라고 한다면 음극은 0 V로 간주할 수 있어요.
이러한 관점을 유지하면 그림에서 a,~b,~c점은 모두 10 V가 됩니다. 이와 유사하게 f,~e,~d점은 모두 0 V가 될거에요.
그렇다면 c점이 10V이고, d점이 0V라면, 저항을 거치면서 전압이 10 V만큼 내려가야 한다는 것을 알 수 있어요.
이와 같이 저항을 거치면 전압이 낮아지게 되는데요. 이것을 ‘전압강하’라고 합니다. 또는 ‘저항 양단의 전위차’, ‘저항에 걸린 전압’이라는 용어를 사용하기도 해요.
2-2. 옴의 법칙
[그림 3]과 같이 회로에 기전력원 V와 저항 R이 있다면 회로를 통과하는 전류 I는 어떻게 구할 수 있을까요?
이때 사용하는 법칙이 아래 (2-1)식으로 주어진 옴의 법칙입니다.
\tag{2-1}
I={V \over R}[그림 3]에 주어진 수치를 대입해서 회로를 통과하는 전류 I를 구하면 다음과 같이 0.67 A가 됩니다.
\tag{2-2}
\begin{aligned}
I&={{10~\rm V}\over{15 ~\rm \Omega}}\\[10pt]
&=0.67~\rm A
\end{aligned}3. 저항기 직렬 및 병렬연결과 합성저항
3-1. 저항기의 직렬 연결
아래 [그림 4]는 세개의 저항기가 직렬로 연결된 모습이에요. 여기에서도 직류전원의 전압은 10 V입니다.
이때 회로를 통과하는 전류 I를 구해야 한다고 생각해봐요.
이때 전류가 흐를 수 있는 도선이 한 경로뿐이므로 전류 I는 모든 저항에서 같을 거에요.
![[그림 4] 저항기 직렬 연결](https://ballpen.blog/wp-content/uploads/2024/06/저항기의-직렬연결-1-1024x415.jpg)
전류 I를 구하기 위해서는 (2-1)식으로 주어진 옴의 법칙을 적용하면 되는데요. 전압은 V=10~\rm V로 분명합니다. 문제는 저항 R은 무슨 값을 대입해야 하는지를 알지 못한다는 거에요.
[그림 3]에서는 저항이 하나 뿐이라 명백한데 [그림 4]는 저항이 세개나 되기 때문이죠.
이때 필요한 개념이 합성 저항입니다. 즉 저항이 직렬연결되었을 때 그 전체를 단일의 저항값으로 간주한다면 얼마이냐 하는거에요.
합성 저항 구하는 식을 도출하기 위해서는 위에서 설명드린 전압강하를 우선 상기해봐요.
[그림 4]에서 전원이 10 V이므로 R_1저항의 왼쪽 단자가 10 V이어야 하고, R_3 저항의 오른쪽 단자는 0V가 되야 해요. 그 말은 저항 3개를 거치면서 각각의 저항에서 일어나는 전압강하의 합이 전원전압 V와 같아야 한다는 의미죠.
이를 식으로 쓰면 다음과 같아요.
\tag{3-1}
\begin{align}
V = V_1 + V_2 +V_3
\end{align}그리고 옴의 법칙을 적용하여 전개하면 다음의 결론을 얻을 수 있어요. 이때 전류는 모두 같다는 것을 꼭 기억하세요.
\tag{3-2}
\begin{aligned}
V &= V_1 + V_2 +V_3\\[10pt]
&=IR_1 + IR_2 + IR_3\\[10pt]
&=I(R_1 + R_2 + R_3)\\[10pt]
\end{aligned}그럼 다시 처음으로 돌아가서 우리가 궁금했던 것은 옴의 법칙을 통해 [그림 4]의 회로를 통과하는 전류 I를 구하는 거였어요. 이때 저항값을 얼마로 대입해야 하는 지를 알 수 없었는데요.
위 (3-2)식을 I에 대해 풀면 그 해답을 알 수 있습니다.
\tag{3-3}
I = {V \over {R_1 + R_2 + R_3}}그것은 저항이 직렬연결되었을 때 아래 식과 같이 각 저항의 합을 통해 전체 합성 저항 R_{\rm T}을 구할 수 있어요.
\tag{3-4}
R_{\rm T} = R_1 + R_2 + R_3[문제 풀이]
그럼 [그림 4] 회로를 통과하는 전류를 구해 볼게요.
\tag{3-5}
\begin{aligned}
I &= {V \over R_{\rm T}} \\[10pt]
&={V \over{R_1 + R_2 + R_3}}\\[10pt]
&={{10~V}\over{2.0~\rm \Omega + 3.0~\rm \Omega + 4.0~\rm \Omega}}\\[10pt]
&=1.11~\rm A
\end{aligned}또한 [그림 4]의 각 저항기 양단에서의 전압강하도 구해 볼게요.
\tag{3-6}
\begin{aligned}
&V_1 = I R_1 = 1.11~\rm A \times 2.0~\Omega = 2.22~\rm V\\[6pt]
&V_2 = I R_2 = 1.11~\rm A \times 3.0~\rm \Omega = 3.33~\rm V\\[6pt]
&V_3 = I R_3 = 1.11~\rm A \times 4.0~\rm \Omega = 4.44~\rm V
\end{aligned}각 저항에서의 전압강하의 합이 전원전압 10 V와 같다는 것을 알 수 있어요.
3-2. 저항기의 병렬 연결
다음 [그림 5]는 세개의 저항기들이 병렬연결된 모습을 나타내고 있어요.
여기서도 회로 전체를 통과하는 전류 I를 구한다고 생각해봐요. 그러면 (2-1)식의 옴의 법칙을 적용하면 되는데요. 그런데 문제는 여기서도 저항값을 얼마로 대입해야 하느냐를 알지 못한다는 거에요.
이 말은 저항기들이 병렬연결되었을 때 합성 저항 구하는 방법을 알아야 옴의 법칙을 적용할 수 있게 된다는 뜻입니다.
![[그림 5] 저항기 병렬 연결](https://ballpen.blog/wp-content/uploads/2024/06/저항기의-병렬연결-1-1024x633.jpg)
다만 시작에 앞서 직렬연결에서는 각 저항기를 통과하는 전류가 모두 같았는데요. 병령연결에서는 각 저항기들에 걸린 전압이 모두 같아요.
즉 [그림 5]의 각 저항기들 왼쪽 단자는 10 V이고, 오른쪽 단자는 0 V이어야 하므로 모두 똑같이 10 V의 전압강하가 일어나게 됩니다.
또한 직렬연결에서는 각 저항기에서의 전압강하의 합이 전체 전압과 같았는데요. 병렬연결에서는 그림에 표시한 것처럼 각 저항기를 통과한 전류의 합이 전체 전류와 같아야 해요.
그래서 아래 식이 성립합니다.
\tag{3-7}
I = I_1 + I_2 + I_3윗 식만 풀면 전체 회로를 통과하는 전류 I를 구할 수 있어요. 이때 각 저항기에 걸린 전압이 전원전압 V와 같으므로 더 구체적으로 전개하면 아래와 같습니다.
\tag{3-8}
\begin{aligned}
I&=I_1 + I_2 + I_3\\[6pt]
&={V \over R_1} + {V \over R_2} + {V \over R_3}\\[6pt]
&=V\Big({1 \over R_1 } +{1 \over R_2} + {1 \over R_3} \Big)\\[6pt]
\end{aligned}위 (3-8)식의 마지막 줄을 옴의 법칙 형태로 바꾸기 위해 괄호안 수식을 1 \over {R_{\rm T}}로 치환해볼게요.
\tag{3-9}
{1 \over {R_{\rm T}}} = {1 \over R_1 } + {1 \over R_2} + {1 \over {R_3}}그러면 (3-8)식은 다음과 같이 표현됩니다.
\tag{3-10}
I= {V \over R_{\rm T}}여기서 중요한 것은 (3-9)식의 R_{\rm T}를 통해 전체 전류를 구할 수 있게 된다는 거에요. 그래서 R_{\rm T}를 병렬연결에서의 합성저항이라고 부릅니다.
[문제 풀이]
그럼 [그림 5]를 통과하는 전체 전류 I를 구해볼게요. 이를 위해서는 (3-9)식을 통해 합성저항부터 구해야 합니다.
\tag{3-11}
\begin{aligned}
{1 \over {R_{\rm T}}} &= {1 \over R_1} + {1 \over R_2} + {1 \over R_3}\\[10pt]
&={1 \over {2.0~\rm \Omega}} + {1 \over {3.0~\rm \Omega}} + {1 \over {4.0~\rm \Omega}}\\[10pt]
&={12 \over {24 ~\Omega}} + {8 \over {24~\Omega}} + {6 \over {24~\Omega}}\\[10pt]
&={{26}\over{24~\Omega}}\\[10pt]
\end{aligned}윗식에서 R_{\rm T}를 구하면 다음과 같습니다.
\tag{3-12}
R_{\rm T} = 0.92~\rm \Omega이제 (3-10)식을 적용하면 전체 전류 I를 구할 수 있어요.
\tag{3-13}
\begin{aligned}
I&={V \over R_{\rm T}}\\[10pt]
&={{10~\rm V}\over{0.92 ~\Omega}}\\[10pt]
&\approx10.8~\rm A
\end{aligned}이번에는 각 저항을 통과하는 전류를 구해 볼게요.
\tag{3-14}
\begin{aligned}
&I_1 = {{V}\over{R_1}} = {{10~\rm V}\over{2.0~\Omega}} = 5.0~\rm A\\[10pt]
&I_2 = {{V}\over{R_2}} = {{10~\rm V}\over{3.0~\Omega}} = 3.3~\rm A\\[10pt]
&I_3 = {{V}\over{R_3}} = {{10~\rm V}\over{4.0~\Omega}} = 2.5~\rm A
\end{aligned}앞서 설명드렸듯이 각 저항을 통과하는 전류의 합이 전체전류 10.8 A와 같다는 것을 알 수 있어요.