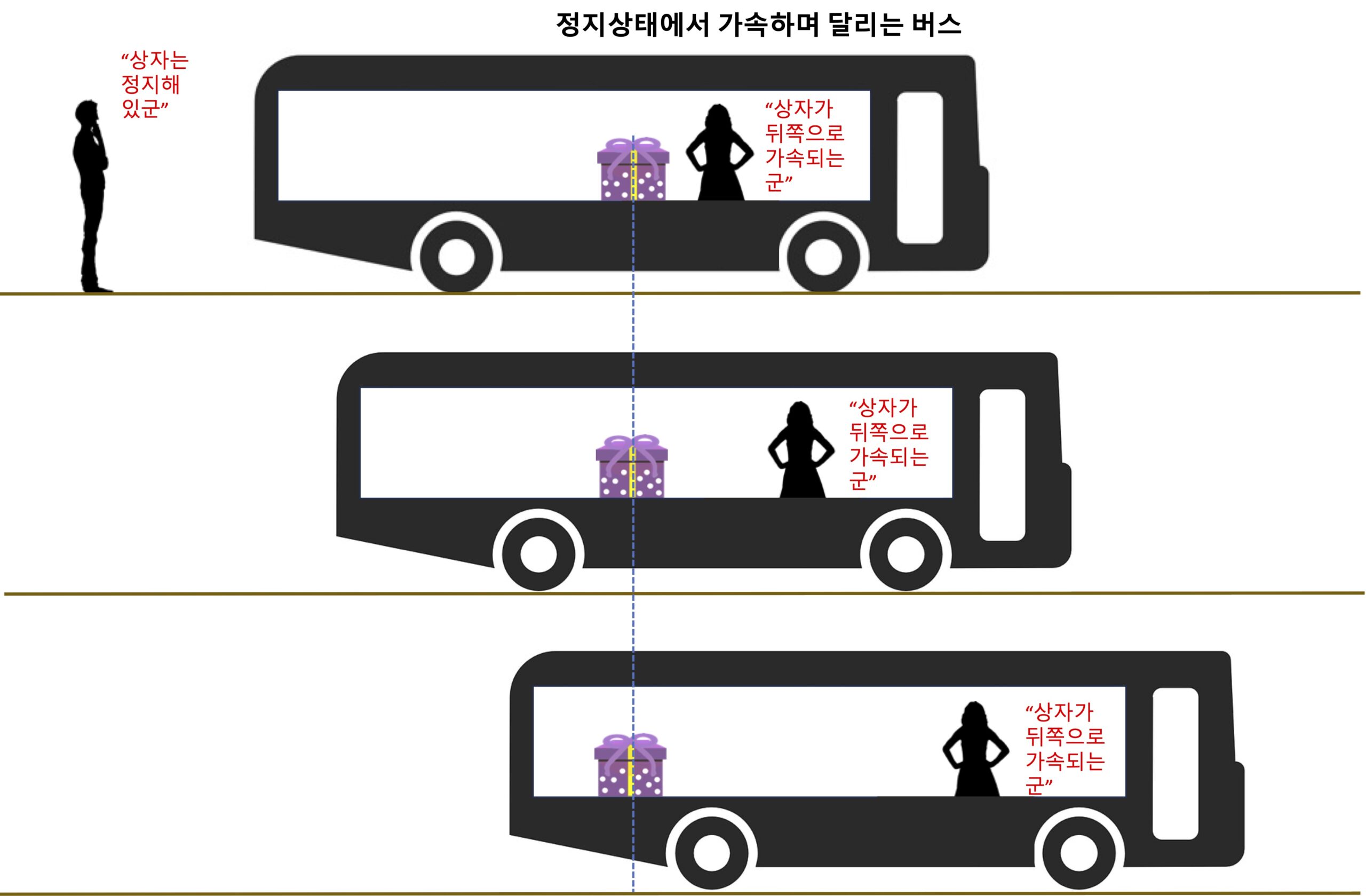
관성력 (겉보기힘, 가상력)5 (1)
관성과 관성력, 관성계와 비관성계의 차이, 그리고 관성력이란 무엇이고 언제 나타나는지 알아 봐요. 관성력(inertial force)은 관성(inertia)과는 다른 개념이에요. 관성력은 힘을 의미합니다. 그런데 이 힘은 실제로 존재하는 힘이 아니에요. 그런데 마치 힘이 실제 존재하는 것처럼 관찰됩니다. 이 힘은 비관성계에서 물체의 관성때문에 나타나요. 그래서 이 힘을 관성력이라고 불러요. 또는 겉보기로만 존재하는 힘이라는 의미에서 겉보기력, 가상적으로만 존재하는 힘이라고 하여 … Read more