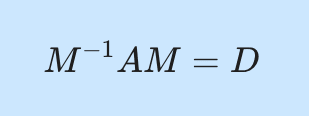Last Updated on 2024-10-13 by BallPen
행렬의 대각화 개념에 대해 알아 봐요.
행렬의 대각화(diagonalization of matrices)란 대칭 선형 변환 행렬 A에 고유벡터로 구성된 직교행렬 M을 아래 식과 같이 적용하면, 고유값 \lambda로 구성된 대각행렬 D가 얻어지는 것을 말합니다.
\tag{D1}
M^{-1}AM = D이 글에서는 위 (D1)식이 어떻게 유도되고, 행렬의 대각화 의미와 예제를 풀어보겠습니다.
아래는 이번 글의 목차입니다.
Contents
1. 고유값 문제 복습
어떤 벡터 \vec x를 행렬 A로 선형변환했을 때 그 결과가 벡터 \vec x의 스칼라 \lambda 배를 만족하는 경우가 있어요.
이를 식으로 쓰면 아래 (1-1)식과 같고, 이것을 고유값 문제(또는 고유치 문제)라고 해요.
\tag{1-1}
A \vec x = \lambda \vec x위 식에서 \lambda는 행렬 A의 고유값, \vec x는 \lambda에 대응하는 고유벡터라고 해요.
예를 들어 행렬 A가 3×3행렬이고 벡터 \vec x가 x_1,~ x_2,~ x_3의 방향성분으로 구성된 3차원 벡터라고 했을 때 (1-1)식은 다음과 같아요.
\tag{1-2}
\begin{pmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{pmatrix}
\begin{pmatrix}
x_1\\
x_2 \\
x_3
\end{pmatrix}
=\lambda
\begin{pmatrix}
x_1\\
x_2\\
x_3
\end{pmatrix}그리고 고유값 문제를 푼다는 의미는 윗 식을 만족하는 세개의 고유값 \lambda_1,~\lambda_2, ~\lambda_3를 구하고, 그에 대응하는 세개의 고유벡터 \vec x,~\vec y, ~\vec z를 구하 것을 의미하죠.
\tag{1-3}
\begin{align}
\vec x =
\begin{pmatrix}
x_1 \\
x_2 \\
x_3
\end{pmatrix}
,~~~
\vec y =
\begin{pmatrix}
y_1 \\
y_2 \\
y_3
\end{pmatrix}
,~~~
\vec z =
\begin{pmatrix}
z_1 \\
z_2 \\
z_3
\end{pmatrix}
\end{align}구체적인 풀이 과정은 이전 고유값 문제에 대한 글을 참고해 주세요.
2. 행렬의 대각화
고유값 문제를 복습했으니 이제부터는 행렬의 대각화 이야기를 시작합니다. 먼저 행렬 대각화를 하는 이유부터 알아봐야겠죠.
2-1. 행렬의 대각화를 하는 이유
(1-2)식에 주어진 3×3행렬을 대각행렬로 바꿀 수 있다면 (1-2)식은 다음과 같아요. 이때 원래의 행렬이 대각행렬로 바뀌었으므로 벡터 \vec x의 x_1,~ x_2,~ x_3의 성분들도 x_1^{\prime},~ x_2^{\prime},~ x_3^{\prime}으로 바뀌었어요.
\tag{2-1}
\begin{pmatrix}
{a_{11}}^{\prime} & 0 & 0\\
0 & {a_{22}}^{\prime} &0 \\
0 & 0 & {a_{33}}^{\prime}
\end{pmatrix}
\begin{pmatrix}
{x_1}^{\prime}\\
{x_2}^{\prime} \\
{x_3}^{\prime}
\end{pmatrix}
=\lambda
\begin{pmatrix}
{x_1}^{\prime}\\
{x_2}^{\prime}\\
{x_3}^{\prime}
\end{pmatrix}그리고 (2-1)식을 전개하면 다음과 같이 대각행렬의 각 성분이 고유값이 된다는 것을 알 수 있습니다.
\tag{2-2}
\begin{align}
&{a_{11}}^{\prime} {x_1}^{\prime} = \lambda_1 {x_1}^{\prime}\\
&{a_{22}}^{\prime} {x_2}^{\prime} = \lambda_2 {x_2}^{\prime}\\
&{a_{33}}^{\prime} {x_3}^{\prime} = \lambda_1 {x_3}^{\prime}
\end{align}\tag{2-3}
\begin{align}
& {a_{11}}^{\prime} = \lambda_1\\
& {a_{22}}^{\prime} = \lambda_2\\
&{a_{33}}^{\prime} = \lambda_3
\end{align}그렇다면 선현 변환행렬을 어떻게 대각행렬로 바꿀 수 있을까요? 이에 대해서는 아래에 계속 설명드리겠습니다.
2-2. 행렬의 대각화 방법 : 닮음변환
고유값 문제 (1-1)을 아래에 다시 쓸게요.
\tag{2-4}
A \vec x = \lambda \vec x그리고 이 식을 변형해 볼텐데요.
좌변에서 행렬 A와 벡터 \vec x 사이에 직교행렬(orthogonal matrix) M에 대한 M M^{-1}를 넣어주어도 식은 달라지지 않아요. 그 이유는 M M^{-1}이 단위행렬이 되기 때문이죠.
\tag{2-5}
A (M M^{-1}) \vec x = \lambda \vec x이번에는 위식의 양변 왼쪽에 M^{-1}를 곱해주어 보세요. 이때 \lambda는 스칼라이므로 곱해지는 행렬과 순서를 바꾸어도 상관없어요.
\tag{2-6}
M^{-1} A (M M^{-1}) \vec x = \lambda M^{-1} \vec x그리고 곱셈 순서는 바꾸지 말고 결합만 아래와 같이 새롭게 해봐요.
\tag{2-7}
(M^{-1} A M )(M^{-1} \vec x) = \lambda (M^{-1} \vec x)그리고 좌변의 M^{-1} A M을 A^{\prime}으로, M^{-1} \vec x 를 \vec x^{\prime}로 치환한다면 다음 식처럼 표현됩니다.
\tag{2-8}
A^{\prime} \vec{x^{\prime}} = \lambda \vec{x^{\prime}}위 식을 구체적으로 표현한 것이 (2-1)식이 되는거에요.
이때 M^{-1} A M을 A^{\prime}로 변환하는 것을 닮음변환(similarity transformation)이라고 합니다. 여기서 닮음이란 크기는 변하되 모양은 변하지 않는 것을 뜻하는데요. 이것이 선형변환을 의미하는 것으로 보면 좋아요.
일단 형태적으로 (2-8)식은 (2-1)식과 모양이 같지만, 궁금한게 있을 거에요. 정말 (2-8)식의 A^{\prime}이 (2-1)식처럼 대각행렬이 되느냐 하는 것이죠.
이 말은 선형 변환행렬 A가 어떤 조건을 가질 때 대각행렬이 되느냐와 같은 질문이에요. 이를 직교 대각화 문제(orthogonal diagonalization problem)라고 불러요.
2-3. 직교 대각화 문제
위 (2-8)식에서 M^{-1} A M을 A^{\prime}으로 치환했는데요. 이 A^{\prime}이 대각행렬이 될 A의 조건을 찾고자 해요.
우선 A^{\prime}이 대각행렬이므로 기호 D로 바꾸어 표현하겠습니다. 그리고 M이 직교행렬인데 (1-3)식의 고유벡터들로 구성되었다고 생각해봐요.
그러면 M은 다음과 같아요.
\tag{2-9}
M =
\begin{pmatrix}
x_1 & y_1 & z_1\\
x_2 & y_2 & z_2 \\
x_3 & y_3 & z_3
\end{pmatrix}그러면 다음 식이 성립하기 위한 A의 조건을 살펴보겠습니다.
\tag{2-10}
M^{-1} A M = D위식의 양변 왼쪽에 M을 곱해주고, 오른쪽에 M^{-1}을 곱해주면 다음 식이 성립합니다.
\tag{2-11}
\begin{align}
M(M^{-1} AM)M^{-1}= MDM^{-1}\\
\end{align}그러면 좌변은 A가 되고, 직교행렬은 전치행렬과 역행렬이 같으므로 M^T = M^{-1}이 성립하여 아래와 같이 표현할 수 있어요.
\tag{2-12}
A = MDM^T그런데 위 식만 보아서는 A의 필요 조건이 정확히 보이지 않을 거에요. 그래서 이번에는 A의 전치를 해봐요.
\tag{2-13}
\begin{align}
A^T &= (MDM^T)^T\\
&=(M^T)^T D^T M^T
\end{align}이때 D는 대각행렬이면서 대칭행렬이에요. 그래서 D^T = D가 성립합니다. 그래서 이 관계를 반영하면 윗 식은 다음과 같아요.
\tag{2-14}
\begin{align}
A^T = M D M^T
\end{align}그런데 위 (2-14)식을 잘 보면 (2-12)식의 A와 같아요. 그래서 다음 관계가 성립합니다.
\tag{2-14}
A^T = A이것이 바로 M^{-1} A M이 대각행렬이 되기 위한 A의 조건입니다. 이 조건을 만족하는 행렬은 대칭행렬이에요.
3. 요점 정리
정리하면 행렬 A가 대칭행렬일 때 다음 관계가 성립합니다.
\tag{3-1}
A^{\prime} = M^{-1} A M여기서 M은 고유벡터로 구성된 직교행렬이며, A^{\prime}은 고유값으로 구성된 대각행렬입니다.
4. 행렬의 대각화 예제
[예제]
어떤 선형 변환행렬이 다음과 같이 주어졌을 때 대각행렬을 구하여 고유값을 구해 보세요.
\tag{4-1}
A =
\begin{pmatrix}
5 & -2\\
-2 & 2
\end{pmatrix}이 선형 변환행렬의 고유값에 대응하는 고유벡터들은 다음과 같아요.
\tag{4-2}
\vec x = {1 \over {\sqrt{5}}}
\begin{pmatrix}
-2\\
1
\end{pmatrix}
,~~~
\vec y = {1 \over {\sqrt{5}}}
\begin{pmatrix}
1\\
2
\end{pmatrix}[Solution]
고유벡터로 구성된 직교행렬 M을 정의하면 다음과 같습니다. (2-9)식을 적용하면 됩니다.
\tag{4-3}
M = {1 \over {\sqrt{5}}}
\begin{pmatrix}
-2 & 1\\
1 & 2
\end{pmatrix}이제 행렬의 대각화 계산을 해봐요. (3-1)식을 적용하면 됩니다.
\tag{4-4}
\begin{align}
M^{-1} A M &= {1 \over {\sqrt{5}}}
\begin{pmatrix}
-2 & 1\\
1 & 2
\end{pmatrix}
\begin{pmatrix}
5 & -2\\
-2 & 2
\end{pmatrix}
{1 \over {\sqrt{5}}}
\begin{pmatrix}
-2 & 1\\
1 & 2
\end{pmatrix}\\[10pt]
&={1 \over 5}
\begin{pmatrix}
-2 & 1\\
1 & 2
\end{pmatrix}
\begin{pmatrix}
-12 & 1\\
6 & 2\\
\end{pmatrix}\\[10pt]
&={1 \over 5}
\begin{pmatrix}
30 & 0 \\
0 & 5
\end{pmatrix}
\end{align}윗 식에서 대각선에 있는 두 값이 고유값에 해당합니다. 그러므로 두 고유값은 다음과 같아요.
\tag{4-5}
\lambda_1 = 6,~~~\lambda_2 = 1