가우스 법칙 예제

Last Updated on 2024-05-31 by BallPen

몇가지 가우스 법칙 예제들을 풀어보겠습니다.

가우스 법칙 예제 몇 개를 이번 글에서 풀어볼게요.

가우스 법칙의 적분형은 다음 식으로 주어집니다.

\tag{D1}
\oint \vec E \cdot d \vec a = {{Q_{enc}}\over{\epsilon_0}}

윗 식에서 좌변은 전기장 선속을 뜻하고, 우변의 Q_{enc}는 가우스 면 안쪽의 알짜 전하를 의미하죠.

또한 가우스 법칙의 미분형은 다음과 같아요.

\tag{D2}
\nabla \cdot \vec E = {{\rho}\over{\epsilon_0}}

이제부터 예제를 풀어봐요. 아래는 이번 글의 목차입니다.

1. 가우스 법칙 예제 1 : 무한 평면 전하 분포에 의한 전기장

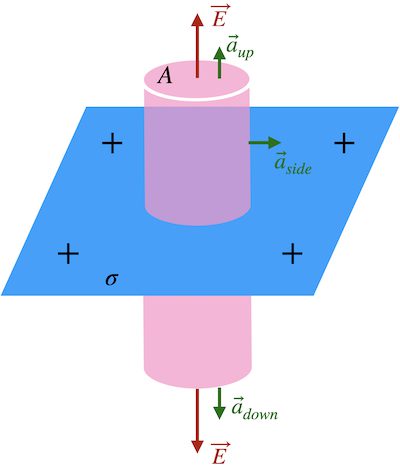
[그림 1]은 무한한 크기를 갖는 평평한 판에 면전하밀도 \sigma가 분포된 것을 나타내고 있어요.

그러면 그 면전하에 의한 전기장은 빨강색 화살표로 나타낸 것처럼 판에 수직한 방향을 향합니다.

물론 판이 무한히 크지 않다면 판의 가장자리에서는 전기장의 수평 성분도 존재하겠죠. 그러나 문제 상황을 간단히 하기 위해 무한한 평면 전하 분포를 가정했어요.

그렇다면 무한 평면 전하 분포에 의한 전기장 \vec E는 어떻게 구할 수 있을까요? 네 맞아요. 가우스 법칙을 이용하면 됩니다.

가우스 법칙을 적용하기 위해서는 닫혀진 3차원의 가우스 면을 설정해야 하는데요. [그림 1]의 분홍색 원통처럼 설정했다고 생각해봐요.

그러면 그 가우스 면을 통과하는 총 전기장 선속은 원통의 윗면, 아래면, 측면을 통과하는 선속의 합이 될거에요. (D1)식을 이용해 구체적으로 전개하면 다음과 같습니다.

\tag{1-1}
\begin{align}
\oint \vec E \cdot d \vec a &= \vec E \cdot  \vec a_{up} +\vec E \cdot  \vec a_{down} + \vec E \cdot  \vec a_{side} \\[10pt]
&= {{Q_{enc}}\over{\epsilon_0}}
\end{align}

이때 전기장 \vec E는 앞에서 말씀드렸듯이 평판이 무한한 크기이므로 평판에 수직한 방향을 향해요.

그러므로 그림에서 빨강색 화살표로 표시한 것처럼 평판의 위쪽에서는 위쪽 방향을, 아래쪽에서는 아래쪽 방향을 향하죠.

그렇다면 가우스 면의 면벡터 \vec a의 방향은 어떨까요?

\vec a_{up}은 가우스 원통의 윗면이 만드는 면벡터로써 전기장의 방향과 평행합니다. 그리고 \vec a_{down}은 원통의 아래면이 만드는 면벡터로써 이 경우에도 전기장의 방향과 평행해요.

반면에 \vec a_{side}는 원통의 측면이 만드는 면벡터인데요. 측면에 수직한 방향이므로 옆쪽을 향하게 되고 결국 전기장의 방향과 항상 수직한 방향이 된다는 것을 알 수 있을 거에요.

그러므로 (1-1)식에서 \vec E \cdot \vec a_{side}는 내적의 규칙에 따라 0이 됩니다.

아울러 \vec a_{up}과 \vec a_{down}의 크기는 원통의 윗면과 아래면 면적으로 서로 동일하니, \vec A로 통일할게요.

그러면 최종적으로 (1-1)식은 다음과 같이 다시 쓸 수 있습니다.

\tag{1-2}
\begin{align}
\oint \vec E \cdot d \vec a &= \vec E \cdot  \vec a_{up} +\vec E \cdot  \vec a_{down}\\[10pt]
&=\vec E \cdot \vec A + \vec E \cdot \vec A \\[10pt]
&=2EA\\[10pt]
&={{Q_{enc}}\over{\epsilon_0}}
\end{align}

결국 (1-2)식의 세번째와 네번째 줄을 정리하면 무한 평판 전하에 의한 전기장 크기는 다음과 같습니다.

\tag{1-3}
E = {{1}\over{2 \epsilon_0}}\Big({{Q_{enc}}\over{A}}\Big)= {{\sigma}\over{2 \epsilon_0}}

이 전기장의 크기를 벡터로 나타내려면 방향을 표시해주어야 하는데요. 평판에 수직한 방향의 단위벡터를 \hat n으로 일반화하면 다음과 같이 최종적으로 표현할 수 있습니다.

\tag{1-4}
\vec E = {{\sigma}\over{2 \epsilon_0}} \hat n

(1-4)식의 결과를 이용하면 + \sigma와 - \sigma로 대전된 평행한 두 금속판 사이의 전기장도 쉽게 구할 수 있어요. 이것도 계속 알아봐요.

[무한 평행판 사이에서의 전기장]

위 [그림 2]는 두개의 서로 마주보는 무한 크기의 평행판을 옆에서 본 모습이에요. 검정색과 빨강색 세로선이 평행판인거죠. 이때 각각의 면전하 밀도는 +\sigma와 - \sigma로 가정하겠습니다.

그러면 검정색 평판에 의한 전기장은 검정색 화살표로 표시한 것처럼 {{\rho}\over{2 \epsilon_0}}의 크기를 갖고 면에 수직하게 나가는 방향을 향합니다.

반대로 빨강색 평판에 의한 전기장은 크기는 동일하지만 빨강색 평판 쪽으로 들어가는 방향으로 생성되죠. 그 이유는 음전하로 대전되어 있기 때문이에요.

그렇다면 그림에서 (i)영역의 전기장은 어떻게 될까요? 네 맞아요. 동일한 크기를 갖되 방향이 반대인 두 전기장이 서로 상쇄되므로 총 전기장은 0이 됩니다.

이와 동일하게 (iii)영역도 0이 되죠.

하지만 (ii)영역은 전기장이 모두 같은 방향을 향하므로 총 전기장의 크기는 다음과 같이 {{\sigma}\over{\epsilon_0}}가 되며, 방향은 양전하에서 음전하를 향합니다..

\tag{1-5}
\vec E_{(ii)} = \Big({{\sigma}\over{2 \epsilon_0}}\Big) \times 2 = {{\sigma}\over{\epsilon_0}}

위 (1-5)식이 무한 평행판 사이에서의 전기장입니다.

2. 가우스 법칙 예제 2 : 균일하게 대전된 구의 전기장

아래 [그림 3]은 반지름 R, 총전하 Q로 균일하게 대전된 구를 나타냅니다.

여기서 균일하게 대전되었다는 의미는 구의 부피전하밀도가 모든 부분에서 상수임을 의미해요.

이 경우 전기장의 방향은 구의 중심에서 방사상으로 나가는 방향을 향하게 됩니다. 이 방향의 단위벡터를 \hat r으로 표기할게요.

이때 반지름 r인 구 내부에서의 전기장과 구 외부에서의 전기장을 구해봐요.

2-1. 구 내부에서의 전기장

먼저 구 내부에서의 전기장을 구해 볼께요.

이를 구하기 위해서는 닫혀진 가우스 면을 설정해야 합니다.

[그림 3]의 왼쪽 그림은 구 내부에 가우스 구면을 설정한 거에요. 그림에서는 점선의 동그란 원으로 그렸습니다만 3차원의 구면을 생각하면 되요.

그러면 그 구면이 만드는 면벡터 방향은 중심에서 나가는 방향을 향하게 되므로 \hat r을 향하게 됩니다.

따라서 구에 의해 형성된 전기장 방향과 가우스 구면의 면벡터 방향은 항상 평행한 것을 상상할 수 있을거에요.

그러면 이제 (D1)식을 이용해 전기장의 크기를 구하면 됩니다. 여기서 가우스 구면의 표면적을 A로, 부피전하밀도는 \rho = {{Q} \over {{4 \over 3} \pi R^3}}로 나타낼게요.

\tag{2-1}
\begin{align}
\oint \vec E \cdot d \vec a &= \vec E \cdot \vec A \\[10pt]
&=\color{blue}E(4 \pi r^2) \\[10pt]
&={{Q_{enc}}\over{\epsilon_0}}\\[10pt]
&= \color{black}\Big( {{4 \over 3} \pi r^3}  \Big)\rho {1 \over {\epsilon_0}}\\[10pt]
&=\color{blue}\Big( {{4 \over 3} \pi r^3}  \Big)\Big({{Q}\over{{{4}\over{3}}\pi R^3}}\Big) {1 \over {\epsilon_0}}
\end{align}

윗 식에서 Q_{enc}는 가우스 구면 내부의 알짜 전하량이므로 해당 가우스 구면의 부피에 부피전하밀도를 곱해주어야 합니다.

식에서 파랑색 부분을 서로 같게 놓고 정리하면 구 내부에서의 전기장 E_{in}은 다음과 같습니다.

\tag{2-2}
\vec E_{in} = {1 \over{4 \pi \epsilon_0}} {Q \over {R^3}} r \hat r 

윗 식에 따르면 균일하게 대전된 구 내부의 전기장은 r 에 비례하는 것을 알 수 있어요.

2-2. 구 외부에서의 전기장

구 외부의 전기장을 구하기 위한 가우스 구면 설정은 [그림 3]의 오른쪽 그림을 보면 됩니다.

여기서도 가우스 법칙을 적용하면 되는데요. 이 경우 Q_{enc}는 Q와 같아요.

\tag{2-3}
\begin{align}
\oint \vec E \cdot d \vec a &= \vec E \cdot \vec A\\[10pt]
&=\color{red}E(4 \pi r^2)\\[10pt]
&={{Q_{enc}}\over{\epsilon_0}}\\[10pt]
&=\color{red}{{Q}\over{\epsilon_0}}
\end{align}

빨강색 부분을 서로 같게 놓고 정리하면 구 외부에서의 전기장 E_{out}은 다음과 같습니다.

\tag{2-4}
\vec E_{out} = {1 \over{4 \pi \epsilon_0}} {Q \over {r^2}} \hat r 

윗 식에 따르면 균일하게 대전된 구 외부의 전기장은 r^2 에 반비례하는 것을 알 수 있어요.

지금까지 균일하게 대전된 구 내부에서의 전기장과 외부에서의 전기장을 (2-2)식과 (2-4)식으로 구했는데요.

반지름 r의 함수로서 전기장 E의 변화를 그래프로 그려보면 다음 [그림 4]와 같아요.

이때 관련된 상수값들은 {1 \over{4 \pi \epsilon_0}} = 9 \times 10^ 9, Q=10, R=3으로 설정했습니다.

구 내부에서는 파랑색 선과 같이 전기장의 크기가 r에 비례하여 증가하고, 구 외부에서는 빨강색 선과 같이 r^2에 반비례하며 급격히 감소합니다.

Related posts.

자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 자동차의 최고출력 개념과 이 값이 크면 무엇이 좋은가? 인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 밀도 정의와 활용 사례 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요. 선풍기 살 때 풍량 효율 큰 것 고르면 되는 거에요?