Last Updated on 2021-12-04 by BallPen
벡터에 스칼라를 곱하여 벡터의 실수배를 연산하는 수학적 방법과 기하학적 의미를 소개합니다.
벡터의 실수배 연산에 대한 내용이 이번 글에서 다루어 집니다.
벡터와 관련된 다른 내용은 아래의 글들을 참고하시기 바랍니다. 순서대로 읽으면 벡터를 이해하는데 크게 도움을 받을 수 있어요.
- 벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분 (클릭)
- 단위벡터 의미와 벡터 정규화 (클릭)
- 벡터의 방향 표기를 정확하게 하는 방법 (클릭)
- 벡터의 덧셈 : 기하학적 표현과 수학적 처리 (클릭)
- 벡터의 뺄셈 : 벡터의 변화량을 구하는 도구 (클릭)
- 벡터의 실수배 : 벡터에 스칼라를 곱하는 방법과 기하학적 의미
아래는 이번 글의 목차입니다.
Contents
1. 벡터의 실수배 연산을 위한 수학적 방법
1-1. 벡터와 스칼라의 차이
벡터의 실수배 연산을 벡터에 스칼라를 곱한다고 표현하기도 합니다. 여기서 벡터란 크기와 방향을 갖는 물리량이고 스칼라는 크기만 갖는 물리량을 말합니다.
예를 들어 벡터는 변위, 속도, 운동량, 힘 등이 있고, 스칼라는 이동거리, 질량, 온도, 면적 등이 있습니다.
더 쉽게 표현하면 벡터는 어느 물리량의 숫자값에 +와 -의 부호가 붙는 것이 특징입니다. 이때 숫자가 크기이고 부호는 방향을 의미합니다.
예를들어 v=+3.0\mathrm{m/s}라는 속도 표현이 있다고 보겠습니다. 여기서 숫자 3.0은 속도의 크기이고 앞에 붙은 부호 +는 방향을 뜻합니다. 이때 +의 방향은 관찰자가 임의로 정하는 것인데요. 오르쪽을 기준방향으로 정했다면 오른쪽이 +가 되고 그 반대방향인 왼쪽은 -가 됩니다.
그렇다면 m=+3.0 \mathrm{kg}은 벡터일까요 아니면 스칼라일까요? kg의 단위를 갖는 질량은 가장 대표적인 스칼라입니다.
이때 숫자 3.0이 질량의 크기에 해당하죠. 그렇다면 +부호는 방향을 뜻할까요? 아니요. 그렇지 않습니다. 단지 양의 값을 갖는다는 것을 의미할 뿐입니다. 질량에서는 – 값이 존재하지 않습니다. 예를들어 여러분에게 -3 kg의 물건을 가져오라고 한다면 황당할 것입니다.
이와 같이 스칼라량은 -의 방향 자체가 존재할 수 없습니다. 결국 스칼라는 크기만 있고 방향이 없는 것이죠.
1-2. 벡터의 양의 실수배
아래의 (1)식으로 표기된 어느 벡터가 있습니다.
\tag{1}
\begin{align}
\vec{A} = A_x \hat{x} + A_y \hat{y}
\end{align}이 벡터에 k라는 양의 실수를 곱하면 어떻게 처리하면 될까요? 바로 벡터 \vec{A}의 각 성분의 크기에 각각 k를 곱하면 됩니다.
\tag{2}
\begin{align}
k \vec{A} &= k(A_x \hat{x} + A_y \hat{y})\\
&=kA_x \hat{x} + kA_y \hat{y}\\
\end{align}1-3. 벡터의 음의 실수배
이번에는 (1)식으로 주어진 벡터에 -k의 음의 실수를 곱한다면 수학적으로 어떻게 처리해야 할까요?
이 경우에는 -1의 부호값과 양의실수 k로 각각 구분해서 생각해야 합니다. 그렇게하면 k는 크기가 되고 -1은 벡터의 방향을 빠꾸는 방향 정보로 보면 됩니다.
아래 (3)식을 참고하세요. (1)식의 벡터에 -k를 곱하는 과정입니다.
\tag{3}
\begin{align}
-k\vec{A} &= (-1)k(A_x\hat{x}+A_y\hat{y})\\
&=k \Big[ A_x (- \hat{x} ) + A_y(-\hat{y}) \Big]\\
&=kA_x (-\hat{x})+kA_y(-\hat{y})
\end{align}(3)식의 마지막 줄과 같이 어느 벡터 \vec{A}에 -k를 곱하면, 각 성분의 크기가 k배되고, 각 성분의 방향이 반대가 된다는 것을 알 수 있습니다.
2. 벡터의 실수배 연산에 대한 기하학적 의미
2-1. 벡터의 양의 실수배
(4)식에 벡터 \vec{A}가 있습니다. 이 벡터에 실수 2를 곱하여 2\vec{A}를 연산한다면 기하학적으로 어떠한 의미를 가질까요?
\tag{4}
\begin{align}
\vec{A} = 3.25\hat{x} + 4.34\hat{y}
\end{align}(4)식의 벡터에 실수 2를 곱하면 위에서 말씀드렸듯이 벡터를 구성하는 각 성분의 크기에 2를 곱하는 것과 같습니다.
\tag{5}
\begin{align}
2\vec{A} &= 2(3.25 \hat{x} + 4.34 \hat{y})\\
&=6.50 \hat{x} + 8.68 \hat{y}\\
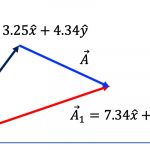
\end{align}그렇다면 (4)식의 원래 벡터와 실수 2가 곱해진 (5)식의 벡터는 기하학적으로 어떠한 차이가 있을까요? [그림 1]과 같이 각 벡터를 그림으로 그려보면 쉽게 알 수 있습니다.
![[그림 1] 벡터의 실수배 연산. 벡터 <span class="katex-eq" data-katex-display="false">\vec{A}</span>에 실수 2를 곱하면 벡터 <span class="katex-eq" data-katex-display="false">\vec{A}</span>와 방향은 동일하지만 크기가 2배 증가한 벡터가 형성됩니다.](https://ballpen.blog/wp-content/uploads/2021/11/Picture1-4.jpg)
[그림 1]과 같이 벡터 \vec{A}에 실수 2를 곱하면 벡터 \vec{A}와 방향은 동일하지만 크기가 2배인 새로운 벡터가 만들어 집니다.
결국 어느 벡터에 양의 실수를 곱하면 방향은 그대로 유지된 상태에서 실수값 만큼 크기가 변한 벡터가 얻어집니다.
예를 들어 실수값 3.5가 어느 벡터에 곱해진 경우 원래 벡터보다 크기가 3.5배 큰 벡터가 얻어집니다. 또한 실수값 0.5가 곱해진 경우 원래 벡터보다 크기가 1/2만큼 작아진 벡터가 얻어지게 되는 것이죠.
2-2. 벡터의 음의 실수배
이번에는 (4)식의 벡터에 -0.7의 음의 실수를 곱한다면 어떻게 될까요? 바로 아래 (6)식처럼 수학적으로 계산할 수 있습니다.
\tag{6}
\begin{align}
-0.7\vec{A} &= -0.7(3.25 \hat{x} + 4.34 \hat{y})\\
&=0.7\big[ 3.25(-\hat{x}) + 4.34(-\hat{y}) \big]\\
&=2.28 (-\hat{x}) + 3.04 (-\hat{y})\\
\end{align}그렇다면 (4)식의 벡터와 -0.7이 곱해진 (6)식의 벡터는 기하학적으로 어떠한 차이가 있을까요? 아래 [그림 2]를 보아주세요.
![[그림 2] 벡터의 실수배 연산. 벡터 <span class="katex-eq" data-katex-display="false">\vec{A}</span>에 실수 -0.7를 곱하면 벡터 <span class="katex-eq" data-katex-display="false">\vec{A}</span>와 방향이 반대이고 크기가 0.7배 감소한 벡터가 형성됩니다.](https://ballpen.blog/wp-content/uploads/2021/11/Picture2-4.jpg)
[그림 2]와 같이 벡터 \vec{A}에 실수 -0.7를 곱하면 벡터 \vec{A}와 방향이 반대이고 크기가 0.7배 감소한 벡터가 새로운 벡터가 만들어집니다.
3. 벡터의 실수배 연산 요약
- 벡터에 양의 실수 k를 곱하면 수학적으로 벡터의 각 성분 크기에 k가 곱해진다. 따라서 원래벡터와 비교하여 크기가 k배 변하고 방향은 그대로 유지된 벡터가 형성된다.
- 벡터에 음의 실수 -k를 곱하면 수학적으로 벡터의 각 성분 크기에 k가 곱해지고 단위벡터에는 (-1)이 곱해져 방향이 반대가 된다. 따라서 원래벡터와 비교하여 크기가 k배 변하고 방향은 반대인 벡터가 형성된다.
- 벡터의 크기는 항상 양수(절대값)이고, 부호는 단위벡터의 방향정보에 반영된다.




2 thoughts on “벡터의 실수배 : 벡터에 스칼라를 곱하는 방법과 기하학적 의미”