전기쌍극자 (Electric dipole)

BallPen · 2022-10-09T11:20:19+09:00

전기쌍극자(electric dipole)에는 유도형과 배향형 쌍극자가 있어요. 전기쌍극자는 전하량의 크기가 같은 양전하와 음전하가 거리를 두고 놓여 있어요. 그래서 외부 전기장에 의해 민감하게 반응합니다. 전기쌍극자가 만드는 전기장과 전위를 유도해 봐요.

Last Updated on 2022-10-09 by BallPen

전기쌍극자가 만드는 전위, 전기장에 대해 알아보겠습니다.

전기쌍극자(electric dipole)란 전하량이 같은 양전하와 음전하가 서로 공간적으로 분리되어 존재하는 것을 말합니다.

이번 글에서는 전기쌍극자가 만드는 전위와 전기장에 대해 이야기 하겠습니다.

아래는 이번 글의 목차입니다.

Contents

1. 전기쌍극자
2. 전기쌍극자 전기장
- 2-1. 점전하에 의한 전기장
- 2-2. 전기쌍극자가 만드는 전기장
3. 전기쌍극자 전위
- 3-1. 점전하에 의한 전위
- 3-2. 전기쌍극자가 만드는 전위
[부록] 전위의 기울기로 전기장 구하기

1. 전기쌍극자

전기쌍극자(electric dipole)는 크게 두가지 원인에 의해 나타납니다.

첫번째는 지난 글에서 설명드린 것처럼 외부 전기장에 의해 원자 중심의 핵과 주변을 돌고 있는 전자의 회전 중심이 상대적으로 변화되어 나타납니다. 이것을 ‘유도형 전기쌍극자’라고 부릅니다.

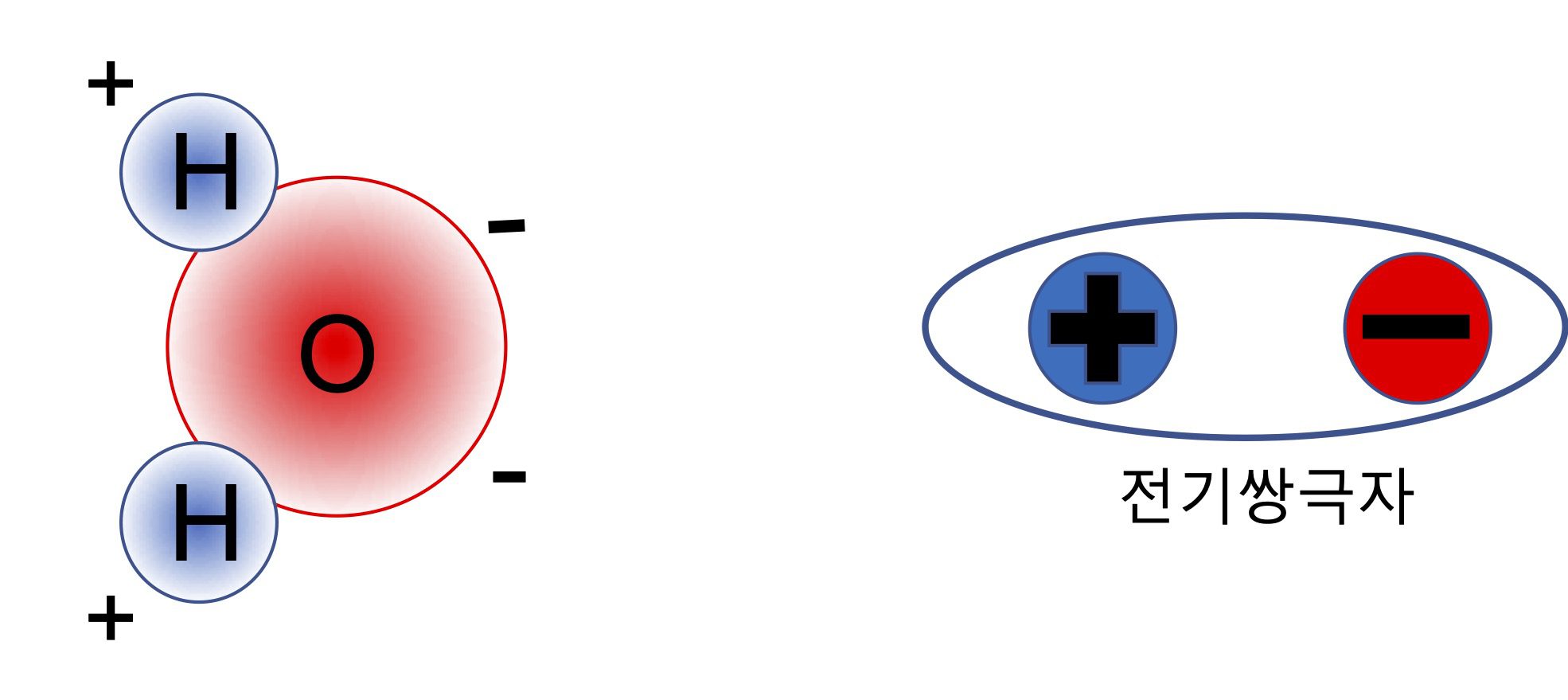
두번째는 극성을 갖는 분자에서 주로 나타납니다. 극성분자의 대표적인 예가 물 분자에요.

아래 [그림 1]에서 왼쪽 그림은 물 분자의 모형입니다.

물 분자는 그림과 같이 양전하와 음전하의 중심이 일치하지 않고 양 끝쪽으로 각각의 극성을 갖고 있습니다. 그래서 이런 분자를 멀리서 보게 되면 [그림 1]의 오른쪽 그림과 같이 전기쌍극자로 간주 할 수 있어요.

이러한 것을 분자 배치에 의한 전기쌍극자라고 하여 ‘배향형 전기쌍극자’라고 합니다.

전기쌍극자가 재미있는 이유는 외부에서 걸어준 전기장에 민감하게 반응한다는 것입니다. 대표적으로 부도체에서의 유전 분극 현상이 있어요.

그렇다면 이러한 전기쌍극자가 만드는 전위와 전기장에 대해 알아봐요.

2. 전기쌍극자 전기장

전기쌍극자가 만드는 전기장을 유도하기 위해서는 우선 점전하에 의한 전기장을 알아야 합니다.

2-1. 점전하에 의한 전기장

점처럼 아주 작은 크기를 갖는 점전하(point charge)로부터 어느 거리만큼 떨어진 곳에서의 전기장을 구해보겠습니다. 아래 [그림 2]를 보아 주세요.

[그림 2]는 원점으로부터 위치벡터 $\vec{r_1}$ 인 곳에 전하량 $q$ 인 점전하가 놓여 있어요. 그리고 위치벡터 $\vec{r_2}$ 인 곳에 점 $P$ 가 있습니다.

그러면 점전하로부터 점 $P$ 를 향하는 벡터는 벡터의 뺄셈 규칙에 따라 $\vec{r_2} - \vec{r_1}$ 이 됩니다.

[그림 2] 양전하로부터 <span class="katex-eq" data-katex-display="false">\vec{r_2} - \vec{r_1}</span>만큼 떨어진 <span class="katex-eq" data-katex-display="false">P</span>점에서의 전기장 — [그림 2] 양전하로부터 $\vec{r_2} - \vec{r_1}$ 만큼 떨어진 $P$ 점에서의 전기장

이 상황에서 $P$ 점에서의 전기장은 다음과 같이 정의됩니다.

\tag{1} \begin{align} \color{blue}\vec{E} = k{{q}\over{|\vec{r_2}-\vec{r_1}|^3}} (\vec{r_2}-\vec{r_1}) \end{align}

이때 $k$ 는 $1/{4 \pi \epsilon_0}$ 로서 $8.99\times 10^9~\mathrm{N \cdot m^2 / C^2}$ 의 값을 갖는 상수입니다.

(1)식을 보면 통상적으로 점전하로부터 거리 $r$ 만큼 떨어진 곳에서의 전기장을 구하는 아래의 (2)식과는 다른 모양처럼 보일 수 있어요.

\tag{2} \vec{E} = k {{q}\over{r^2}} \hat{r}

그런데 식 (1)을 다음과 같이 표현을 바꾸면 (2)식과 동일한 모양을 갖습니다.

\tag{3} \begin{align} \vec{E} &= k{{q}\over{|\vec{r_2}-\vec{r_1}|^3}} \color{red}(\vec{r_2}-\vec{r_1})\\ &=k{{q}\over{|\vec{r_2}-\vec{r_1}|^{\cancel{3}\color{red}2}}} \color{red} \cancel{|\vec{r_2}-\vec{r_1}|}(\hat{\vec{r_2}-\vec{r_1}})\\ &=k{{q}\over{|\vec{r_2}-\vec{r_1}|^{\color{red}2}}} \color{red}(\hat{\vec{r_2}-\vec{r_1}}) \end{align}

즉, 벡터 $({\vec{r_2} - \vec{r_1}})$ 을 크기인 ${|\vec{r_2}-\vec{r_1}|}$ 과 단위벡터 $\hat{\vec{r_2} - \vec{r_1}}$ 으로 분해하여 표현할 수 있어요.

그리고 그 크기는 분모와 약분됩니다. 그리고 $({\vec{r_2} - \vec{r_1}})$ 을 $({r})$ 로 치환하면 (2)식과 같아지게 됩니다.

그런데 (2)식처럼 간단하게 표현하지 왜 (1)식처럼 복잡하게 표현할까요? 그 이유는 점전하가 하나인 경우에는 그 점전하를 원점에 두고 (2)식처럼 표현하는게 편리해요. 그러나 점전하가 하나가 아니고 여러 개인 경우 어느 전하를 원점으로 잡을 건지에 대한 고민이 발생합니다.

그래서 이런 경우에는 [그림 2]와 같이 제3의 위치를 원점으로 설정하고 그 원점으로부터 각 점전하의 위치 등에 대해 기술할 수 밖에 없어요.

따라서 다소 복잡해 보이기는 하지만 (2)식보다는 (1)식이 더욱 고도화되고 엄밀하며 더욱 일반적인 표현으로 볼 수 있어요.

2-2. 전기쌍극자가 만드는 전기장

아래 [그림 3]은 전기쌍극자가 $P$ 점에 형성하는 전기장을 구하기 위해 필요한 각 요소의 위치벡터를 나타냅니다. 이때 벡터의 덧셈과 벡터의 뺄셈에 대한 규칙이 적용되었습니다.

[그림 3] 전기쌍극자가 <span class="katex-eq" data-katex-display="false">P</span>에 형성하는 전기장. 전기쌍극자 전하사이의 거리에 비해 전기쌍극자로부터 <span class="katex-eq" data-katex-display="false">P</span>점까지의 거리가 무척 큽니다. — [그림 3] 전기쌍극자가 $P$ 에 형성하는 전기장. 전기쌍극자를 구성하는 전하사이의 거리에 비해 전기쌍극자로부터 $P$ 점까지의 거리가 무척 큽니다.

몇가지 중요한 배치들을 말씀드리면, 전기쌍극자를 구성하는 양전하와 음전하의 전하량 크기는 $q$ 로 동일합니다. 그리고 이 두 전하는 거리 $l$ 만큼 떨어져 있어요.

음전하로부터 $P$ 점까지의 거리는 $|\vec{r} - \vec{r'}|$ 이고 그 방향은 $\hat{|\vec{r} - \vec{r'}|}$ 이 됩니다. 또한 양전하로부터 $P$ 점까지의 거리는 $|\vec{r} - \vec{r'}-\vec{l}|$ 이고 그 방향은 $\hat{|\vec{r} - \vec{r'} - \vec{l}|}$ 이 될거에요.

그렇다면 이제 위에서 설명했던 점전하에 의한 전기장인 (1)식을 적용하여 $P$ 점에 형성되는 전기장을 구해봐요. 각 양전하와 음전하가 만드는 전기장을 서로 합하면 될 것입니다.

이를 ‘중첩의 원리’라고 불러요.

우선 양전하가 $P$ 점에 만드는 전기장이에요.

\tag{4} \begin{align} \vec{E}_{+q} = k{{q}\over{|\vec{r}-\vec{r'}-\vec{l}|^3}} (\vec{r}-\vec{r'}-\vec{l}) \end{align}

이번에는 음전하가 $P$ 점에 만드는 전기장이에요.

\tag{5} \begin{align} \vec{E}_{-q} = k{{-q}\over{|\vec{r}-\vec{r'}|^3}} (\vec{r}-\vec{r'}) \end{align}

그러므로 $P$ 점에 형성되는 전기장은 위의 (4)식과 (5)식을 서로 벡터 합하면 됩니다.

\tag{6} \begin{align} \color{blue}{\vec{E}} &\color{blue}= \vec{E}_{+q} + \vec{E}_{-q}\\ &\color{blue}=kq \Big[ {{(\vec{r} - \vec{r'} - \vec{l})}\over{|\vec{r} - \vec{r'} -\vec{l}|^3 }} - {{(\vec{r} - \vec{r'})}\over{|\vec{r} - \vec{r'}|^3}} \Big] \end{align}

(6)식이 바로 우리가 구하고자 하는 최종 답입니다.

그런데 전기쌍극자와 관련된 물리적 개념을 보다 명확히 하기 위해 (6)식을 근사적으로 다른 형태로 바꾸어 보겠습니다. 여기서 근사한다는 말은 정확히 (6)식과 같지는 않지만 거의 비슷하게 표현된다는 뜻이에요.

전기쌍극자는 아주 작아요. 그래서 [그림 3]에서 쌍극자의 음전하로부터 $P$ 점까지의 거리 $|\vec{r}-\vec{r'}|$ 에 비해 두 전하사이의 거리 $l$ 이 무척 작다고 가정하겠습니다.

그러면 (6)식에서의 분모항을 다음과 같이 바꾸어 쓸 수 있어요.

\tag{7} \begin{align} {{1}\over{|\vec{r}-\vec{r'}-\vec{l}}|^3}&={|\vec{r}-\vec{r'}-\vec{l}}|^{-3}\\ &=\Big[|\vec{r}-\vec{r'}-\vec{l}|^2\Big]^{-{{3}\over{2}}}\\ &=\Big[|\vec{r}-\vec{r'}|^2 - 2 (\vec{r}-\vec{r'})\cdot \vec{l} + l^2 \Big]^{-{3 \over 2}}\\ &=\Big[ |\vec{r}-\vec{r'}|^2\big( 1-{{2(\vec{r} - \vec{r'})\cdot \vec{l}}\over{|\vec{r} - \vec{r'}|^2}} +{{l^2}\over{|\vec{r} - \vec{r'}|^2}} \big) \Big]^{- {3 \over 2}}\\ &=|\vec{r}-\vec{r'}|^{-3}\Big[ 1+ \color{red}{\Big(- {{2(\vec{r} - \vec{r'})\cdot \vec{l}}\over{|\vec{r} - \vec{r'}|^2}} +{{l^2}\over{|\vec{r} - \vec{r'}|^2}} \Big) } \color{black} \Big]^{- {3 \over 2}}\\ \end{align}

이때 쌍극자 사이의 거리벡터 $\vec{l}$ 의 크기에 비해 $\vec{r}-\vec{r'}$ 의 크기가 매우 크다고 가정했잖아요. 즉, 전기쌍극자로부터 $P$ 점이 멀리 떨어져 있는 것이죠.

그러면 (7)식에서 빨강색으로 쓰여진 부분은 1보다 매우 작은 크기를 갖게 될거에요. 근사를 위해 (7)식의 가장 마지막 줄에서 대괄호 사이에 있는 부분에 대해 이항정리를 적용하겠습니다..

이항정리는 다음과 같아요. 단 $x$ 의 절대값이 1보다 작을 때 성립합니다.

\tag{8} (1+x)^n = 1 + nx + \cdots

(8)식의 이항 정리를 (7)식의 가장 마지막줄 대괄호에 적용하면 아래와 같이 쓸 수 있습니다.

\tag{9} \begin{align} {{1}\over{|\vec{r}-\vec{r'}-\vec{l}}|^3} &= |\vec{r}-\vec{r'}|^{-3} \Big[ 1+\Big(-{{3}\over{2}}\Big) \Big( -{{2(\vec{r}-\vec{r'})\cdot \vec{l}}\over{|\vec{r} - \vec{r'}|^{2}}}+{{\color{red}l^2}\over{|\vec{r}-\vec{r'}|^2}} \Big)+\cdots \Big]\\ &\approx|\vec{r}-\vec{r'}|^{-3} + {{3(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^5}} \end{align}

이때 (9)식에서 빨강색으로 표기한 $l^2$ 은 매우 작은 $|\vec{l}|$ 을 제곱하니 더 작아집니다. 그래서 $l^2$ 을 0으로 간주하고, 뒤쪽으로 계속 붙는 항들도 매우 작아 모두 무시할 수 있습니다.

이러한 근사의 과정을 거치면 (9)식의 두번째 줄이 됩니다. 이제 (9)식을 (6)식에 대입해서 근사적인 전기장을 구해 봐요.

\tag{10} \begin{align} \vec{E} \color{black} &=kq \Big[ {{(\vec{r} - \vec{r'} - \vec{l})}\over{\color{black}|\vec{r} - \vec{r'} -\vec{l}|^3 }} - {{(\vec{r} - \vec{r'})}\over{|\vec{r} - \vec{r'}|^3}} \Big]\\ &=kq \Big[ {{(\vec{r} - \vec{r'} - \vec{l})}} {\color{red}\Big( |\vec{r}-\vec{r'}|^{-3} + {{3(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^5}} \Big)} - {{(\vec{r} - \vec{r'})}\over{|\vec{r} - \vec{r'}|^3}} \Big]\\ &=kq\Big[ {{(\vec{r} - \vec{r'}-\vec{l})}\over{|\vec{r}-\vec{r'}|^3}} + {{3(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^5}} (\vec{r}-\vec{r'}-\vec{l}) - {{(\vec{r} - \vec{r'})}\over{|\vec{r} - \vec{r'}|^3}} \Big]\\ &=kq\Big[ \cancel{{\vec{r} - \vec{r'}}\over{|\vec{r}-\vec{r'}|^3}} + {{\vec{l}}\over{|\vec{r}-\vec{r'}|^3}}+ {{3(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^5}} (\vec{r}-\vec{r'}-\vec{l}) - \cancel{{(\vec{r} - \vec{r'})}\over{|\vec{r} - \vec{r'}|^3}} \Big]\\ &=kq \Big[ {{3(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^5}} (\vec{r}-\vec{r'}) - {{3(\vec{r}-\vec{r'})\cdot \color{red}l^2}\over{|\vec{r}-\vec{r'}|^5}} - {{\vec{l}}\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ &=kq\Big[ {{3(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^5}} (\vec{r}-\vec{r'}) - {{\vec{l}}\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ &=k\Big[ {{3(\vec{r}-\vec{r'})\cdot \color{blue}q\vec{l}}\over{|\vec{r}-\vec{r'}|^5}} (\vec{r}-\vec{r'}) - {{\color{blue}q\vec{l}}\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ &=k\Big[ {{3(\vec{r}-\vec{r'})\cdot \color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^5}} (\vec{r}-\vec{r'}) - {{\color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ &=k\Big[ {{3\cancel{|\vec{r}-\vec{r'}}|\hat{(\vec{r}-\vec{r'})}\cdot \color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^{\cancel{5}3}}} \cancel{|\vec{r}-\vec{r'}|}\hat{(\vec{r}-\vec{r'})} - {{\color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ &=k\Big[ {{3\hat{(\vec{r}-\vec{r'})}\cdot \color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^3}} \hat{(\vec{r}-\vec{r'})} - {{\color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ \end{align}

(10)식의 5번째 줄에서 빨강색 $l^2$ 은 워낙 작은 값을 갖기 때문에 0으로 간주합니다. 또한 마지막 세 줄에서 보여지는 파랑색 $q\vec{l}$ 을 $\vec{p}$ 로 치환했어요.

그리고 이 $\vec{p}$ 를 전기쌍극자모멘트(electric dipole moment)라고 부릅니다. 이것은 외부 전기장 내에서 전기쌍극자의 회전이나 배치에 큰 영향을 미치게 됩니다.

전기쌍극자가 만드는 전기장의 크기는 거리의 세제곱에 반비례합니다.

3. 전기쌍극자 전위

지금까지 전기쌍극자에 의한 전기장을 구해봤어요. 이제 부터는 전기쌍극자가 만드는 전위(또는 전압이라 불림)를 유도해봐요. 그러기 위해서는 우선 점전하에 의한 전위를 알아야 합니다.

3-1. 점전하에 의한 전위

[그림 4] 양전하로부터 <span class="katex-eq" data-katex-display="false">\vec{r_2} - \vec{r_1}</span>만큼 떨어진 <span class="katex-eq" data-katex-display="false">P</span>점에서의 전위 — [그림 4] 양전하로부터 $\vec{r_2} - \vec{r_1}$ 만큼 떨어진 $P$ 점에서의 전위

[그림 4]의 상황에서 $P$ 점에서의 전위 $V$ 는 다음과 같이 정의됩니다.

\tag{11} \begin{align} \color{blue}V = k{{q}\over{|\vec{r_2}-\vec{r_1}|}} \end{align}

전기장 $\vec{E}$ 가 크기와 방향을 갖는 벡터량인 것과는 달리 전위 $V$ 는 스칼라량입니다. 따라서 여러개의 점전하가 한 점에 만드는 전위를 구할 때 방향을 고려하지 않아도 됩니다.

3-2. 전기쌍극자가 만드는 전위

전기쌍극자가 만드는 전위를 유도해 봐요.

아래 그림은 [그림 3]과 동일한 그림이에요. [그림 3]이 멀리 있어서 다시 넣었어요.

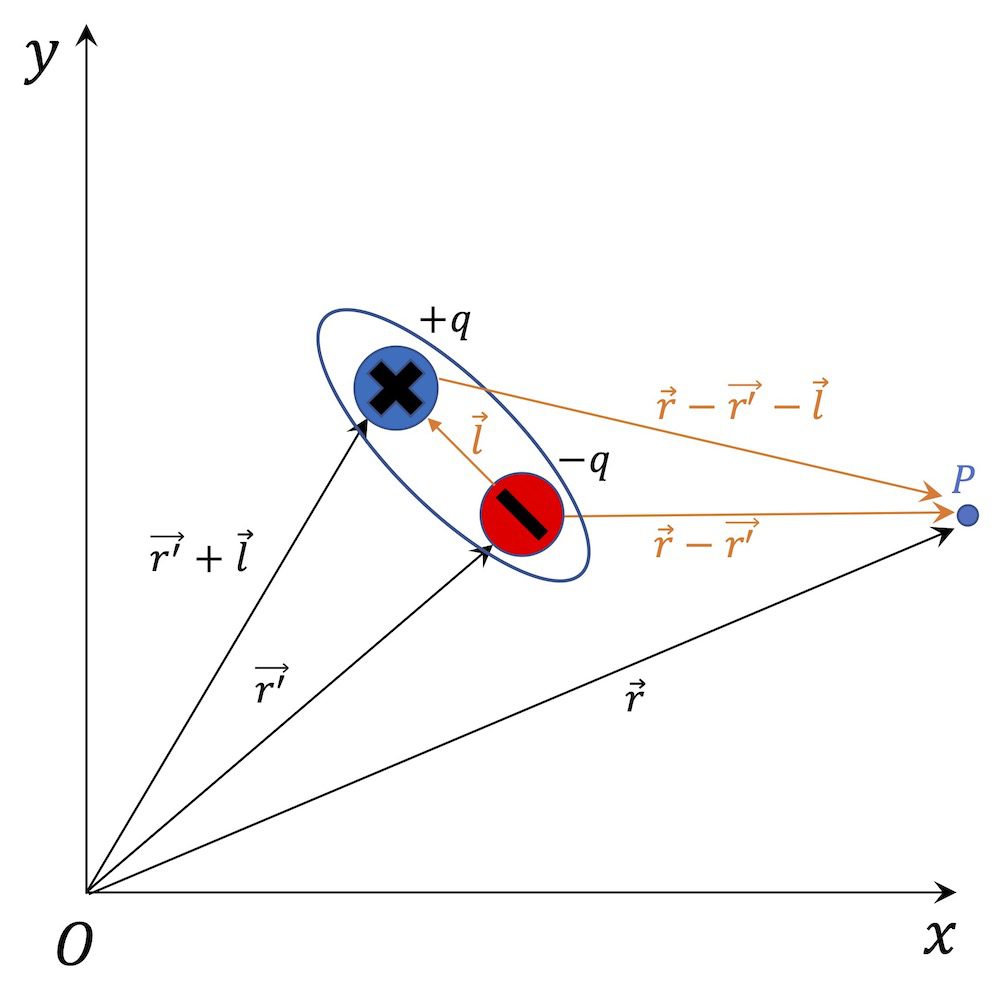
$P$ 점에 형성되는 전위는 양전하와 음전하가 각각 만드는 전위를 합하면 됩니다.

우선 (11)식을 이용해 양전하가 $P$ 점에 만드는 전위에요.

\tag{12} V_{+q} = k{{q}\over{|\vec{r} - \vec{r'}-\vec{l}|}}

이번에는 음전하가 $P$ 점에 만드는 전위에요.

\tag{13} V_{-q} = k{{-q}\over{|\vec{r} - \vec{r'}|}}

그러므로 $P$ 점에 형성되는 전위는 (12)식과 (13)식을 합하면 됩니다.

\tag{14} \begin{align} \color{blue}V &\color{blue}= V_{+q} + V_{-q}\\ &\color{blue}=kq\Big[ {{1}\over{|\vec{r}-\vec{r'}-\vec{l}|}} - {{1}\over{|\vec{r}-\vec{r'}|}} \Big] \end{align}

(14)식이 바로 우리가 구하고자 하는 답입니다.

그런데 전기장을 전기쌍극자모멘트 $\vec{p}$ 로 표현한 것처럼 전위도 전기쌍극자모멘트가 나타나도록 근사해보겠습니다.

여기서도 $P$ 점까지의 거리 $|\vec{r}-\vec{r'}|$ 에 비해 두 전하사이의 거리 $l$ 이 무척 작다고 가정하겠습니다.

우선 (14)식의 첫번째 항을 다음과 같이 바꾸어 봐요.

\tag{15} \begin{align} {{1}\over{|\vec{r}-\vec{r'}-\vec{l}|}} &= |\vec{r} - \vec{r'}-\vec{l}|^{-1}\\ &= \Big[|\vec{r} - \vec{r'}-\vec{l}|^2 \Big]^{-{{1}\over{2}}}\\ &=\Big[ |\vec{r}-\vec{r'}|^2 - 2 (\vec{r}-\vec{r'})\cdot\vec{l} + l^2 \Big]^{-{{1}\over{2}}}\\ &=\Big[|\vec{r}-\vec{r'}|^{2} \big( 1-{{2 (\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^2}}+{{\color{red}l^2}\over{|\vec{r}-\vec{r'}|^2}}\big) \Big]^{-{{1}\over{2}}}\\ &=|\vec{r}-\vec{r'}|^{-1} \Big[1+\Big(-{{2 (\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^2}}\Big)\Big]^{-{{1}\over{2}}}\\ \end{align}

이때 $l^2$ 은 아주 작으므로 0으로 간주하였어요.

(15)식의 마지막 줄에서 대괄호에 대해 이항정리를 적용하여 두번째 항까지만 사용해 봐요. 그러면 아래와 같이 표현됩니다.

\tag{16} \begin{align} {{1}\over{|\vec{r}-\vec{r'}-\vec{l}|}} &\approx |\vec{r}-\vec{r'}|^{-1} \Big[1+\Big({-{{1}\over{\cancel2}}}\Big)\Big(-{{\cancel2 (\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^2}}\Big)\Big]\\ &={{1}\over{|\vec{r}-\vec{r'}}|}+{{(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^3}} \end{align}

이제 (16)식을 (14)식에 대입해서 근사적인 전위를 구해 봐요.

\tag{17} \begin{align} V &= kq\Big[ {{1}\over{|\vec{r}-\vec{r'}-\vec{l}|}} - {{1}\over{|\vec{r}-\vec{r'}|}} \Big]\\ &=kq \Big[\color{red} \cancel{{1}\over{|\vec{r}-\vec{r'}}|}+{{(\vec{r}-\vec{r'})\cdot\vec{l}}\over{|\vec{r}-\vec{r'}|^3}} \color{black}- \cancel{{1}\over{|\vec{r}-\vec{r'}|}} \Big]\\ &=kq{{(\vec{r}-\vec{r'})\cdot \vec{l}}\over{|\vec{r}-\vec{r'}|^3}}\\ &=k{{(\vec{r}-\vec{r'})\cdot \color{blue}q\vec{l}}\over{|\vec{r}-\vec{r'}|^3}}\\ &=k{{(\vec{r}-\vec{r'})\cdot \color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^3}}\\ &=k{{\cancel{|\vec{r}-\vec{r'}|}\hat{(\vec{r}-\vec{r'}})\cdot \color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^{\cancel3 2}}}\\ &=k{{\hat{(\vec{r}-\vec{r'}})\cdot \color{blue}\vec{p}}\over{|\vec{r}-\vec{r'}|^2}}\\ \end{align}

전기쌍극자가 만드는 전위는 거리의 제곱에 반비례합니다.

[부록] 전위의 기울기로 전기장 구하기

전위의 기울기에 -1을 곱하여 전기장을 구할 수 도 있습니다. 이를 식으로 쓰면 다음과 같아요.

\tag{A-1} \vec{E} = - \nabla V

구면좌표계를 적용하면 (A-1)식은 다음과 같이 표현됩니다.

\tag{A-2} \begin{align} \vec{E} &= - \nabla V\\ &=-\Big({{\partial}\over{\partial r}} \hat{r} + {{1}\over{r}}{{\partial}\over{\partial\theta}} \hat{\theta} + {{1}\over{r\sin \theta}} {{\partial}\over{\partial \phi}}\hat{\phi} \Big)V \end{align}

한편, $\hat{({\vec{r}-\vec{r'}})}$ 과 전기쌍극자모멘트 $\vec{p}$ 사이의 각도를 $\theta$ 라고 하면, (17)식의 가장 마지막 식은 다음과 같이 쓸 수 있습니다.

\tag{A-3} \begin{align} V&=k{{\hat{(\vec{r}-\vec{r'}})\cdot \color{black}\vec{p}}\over{|\vec{r}-\vec{r'}|^2}}\\ &=k{{p \cos \theta}\over{|\vec{r}-\vec{r'}|^2}} \end{align}

그러면 (A-3)식을 (A-2)식에 대입해봐요. 이때 (A-3)식에서의 $|\vec{r}-\vec{r'}|$ 는 (A-2)식에서의 $r$ 로 보면 됩니다.

하나씩 분해해서 풀어보겠습니다.

\tag{A-4} \begin{align} {{\partial V}\over{\partial |\vec{r}-\vec{r'}|}} \hat{({\vec{r}-\vec{r'}})} = -2kp\cos\theta{{1}\over{|\vec{r}-\vec{r'}|^3}} \hat{({\vec{r}-\vec{r'}})} \end{align}

\tag{A-5} \begin{align} {{1}\over{|\vec{r}-\vec{r'}|}}{{\partial}\over{\partial\theta}} \hat{\theta} &= {{1}\over{|\vec{r}-\vec{r'}|}}k{{p \sin \theta}\over{|\vec{r}-\vec{r'}|^2}}\hat\theta\\ &=k{{p \sin \theta}\over{|\vec{r}-\vec{r'}|^3}}\hat\theta\\ \end{align}

\tag{A-6} \begin{align} {{1}\over{|\vec{r}-\vec{r'}|\sin \theta}} {{\partial}\over{\partial \phi}}\hat{\phi} = 0 \end{align}

이때 (A-6)식이 0이 되는 이유는 전위에 관한 식이 $\phi$ 에 전혀 의존하지 않기 때문입니다. 바꾸어 말하면 (A-3)식에 $\phi$ 가 하나도 나오지 않아요.

전체적으로 정리하면 다음과 같습니다.

\tag{A-7} \begin{align} \vec{E} &= - \nabla V\\ &=-\Big(-2kp\cos\theta{{1}\over{|\vec{r}-\vec{r'}|^3}} \hat{({\vec{r}-\vec{r'}})} + k{{p \sin \theta}\over{|\vec{r}-\vec{r'}|^3}}\hat\theta \Big)\\ &=k{{1}\over{|\vec{r}-\vec{r'}|^3}} \Big[{{2p \cos \theta}} \hat{({\vec{r}-\vec{r'}})} + {{p \sin \theta}}\hat\theta {\color{red}+ p\cos \theta\hat( \vec{r}-\vec{r'}) -p\cos \theta\hat( \vec{r}-\vec{r'})}\Big]\\ &=k\Big[ {{3p \cos\theta}\over{|\vec{r}-\vec{r'}|^3}} \hat{(\vec{r}-\vec{r'})} + {{\color{red}p(\sin \theta \hat{\theta} - \cos \theta\hat{|\vec{r}-\vec{r'}|)} }\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ &=k\Big[ {{3\hat{(\vec{r}-\vec{r'})}\cdot \color{black}\vec{p}}\over{|\vec{r}-\vec{r'}|^3}} \hat{(\vec{r}-\vec{r'})} - {{\color{black}\vec{p}}\over{|\vec{r}-\vec{r'}|^3}} \Big]\\ \end{align}

(A-7)식의 두번째 줄에서 빨강색으로 표현된 항을 합해주고 빼주었어요.

그리고 세번째 줄에 있는 빨강색 글씨가 전기쌍극자모멘트 벡터가 됩니다. 이것은 전기쌍극자모멘트의 방향을 직각좌표계에서 $z$ 축 방향과 일치시키면 빨강색 글씨의 괄호안에 있는 내용이 $z$ 축 방향의 단위벡터와 같아집니다. 이 경우에는 $\hat{l}$ 이 됩니다.

구면좌표계를 직각좌표계로 표현할 때의 관계식을 찾아보시면 $z$ 축방향의 단위벡터가 빨강색 글씨의 괄호안과 같다는 것을 알게 될거에요.

전위의 기울기로부터 구한 (A-7)식은 (10)식의 전기쌍극자가 만드는 전기장에 관한 식과 동일합니다.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]

5 thoughts on “전기쌍극자 (Electric dipole)”

DS1CLF

2022-10-12 at 9:23 오전

전기공학박사이신가요?
혹시 전기 기술사? 기능장?
암튼 부럽습니다..^^
응답
- BallPen
  
  2022-10-14 at 10:28 오후
  
  많이 부족합니다. 많이 방문해주세요. DS1CLF님 감사합니다.
  응답
- YS
  
  2023-09-18 at 1:55 오후
  
  (편집자가 댓글 일부 수정) 이건 물리학의 전자기학이론이지 전기공학은 응용공학이고 이런 수식을 자세히 가르치지않습니다 실제 진기적인 장치를 만드는데 이론이 많이 필요없고요 전자기학의 대가는 맥스웰포함 엄청많은 믈리학자들이 이야기한거고 전기공힉은 일부만 시용합니다
  응답
  - BallPen
    
    2023-09-18 at 4:01 오후
    
    YS님 저의 블로그를 방문해주시고 관심가져 주셔서 감사합니다. 좋은 하루 되세요.
    응답
Pingback: 전기력선 - ilovemyage