Last Updated on 2023-03-25 by BallPen
특수 상대성 이론에서 나오는 동시성의 상대성 개념을 알아보겠습니다.
동시성의 상대성(Relativity of simultaniety)이란 어느 한 관성기준계에서 동시에 일어난 사건이 다른 관성기준계에서 그 사건을 관찰할 때 동시에 일어나지 않은 것으로 관찰되는 것을 말합니다.
아인슈타인이 특수 상대성 이론을 만들며 제안했던 상대성 원리와 광속 불변의 법칙인 아인슈타인 가정으로 설명되는 현상인데요.
아주 재미있는 개념이 되겠습니다.
함께 알아봐요. 흥미롭고 재미있어요.
아래는 이번 글의 목차입니다.
1. 뉴턴역학의 한계
앞서 말씀드렸듯이 동시성의 상대성은 아인슈타인의 두가지 가정인 상대성 원리와 광속불변의 법칙에 그 뿌리를 두고 있는데요.
어떤 관성기준계에서 동시에 일어난 사건이 다른 관성기준계에서 관찰할 때에도 그 사건이 동시에 일어난 것으로 볼 수 있느냐에 대한 이야기입니다.
아인슈타인의 상대성 이론이 나오기 전 뉴턴(Sir Isaac Newton) 역학이 지배하던 시대에는 상상할 수 없었던 개념입니다.
이 당시에는 어떤 관성기준계에서 동시에 일어난 사건은 다른 관성기준계에서 볼 때에도 동시에 일어나야 하기 때문이었어요.
왜냐하면 뉴턴 역학 시대에는 갈릴레이 변환(Galilean transformation)이 관성기준계 사이에서 공간과 시간의 변환을 위해 사용되었기 때문입니다.
우선 이에 대해 구체적으로 알아 볼 께요.
아래 [그림 1]을 보세요. 케빈(Kevin)과 제니(Jennie)가 있어요.
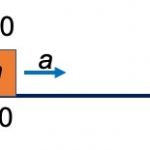
![[그림 1] 제니가 오른쪽으로 등속으로 움직이는 버스안의 중간에 서 있습니다. 그리고 광속 <span class="katex-eq" data-katex-display="false">c</span>인 레이저를 왼쪽과 오른쪽으로 5 m 떨어진 벽을 향해 동시에 발사했어요. 그리고 그 레이저를 버스 밖에 있는 케빈이 관찰하고 있습니다. 케빈이 관찰한 파랑색 레이저의 속도는 광속 <span class="katex-eq" data-katex-display="false">c</span>에 버스의 속도를 더한 값이 되고, 자주색 레이저의 속도는 광속 <span class="katex-eq" data-katex-display="false">c</span>에 버스의 속도를 뺀 값이 됩니다.](https://ballpen.blog/wp-content/uploads/2023/03/갈릴레이-변환1-1024x548.jpg)
케빈 K는 정지상태로 있어요. 그리고 케빈의 입장에서 제니 J는 상대 속도 v_{JK}=0.5~c로 등속으로 달리는 버스 안에 있습니다. 이 말은 케빈과 제니가 있는 공간은 모두 관성기준계로써 물리학 법칙이 동일하게 성립함을 뜻합니다.
여기서 c는 빛의 속도로 3.0 \times 10^8~\mathrm{m/s}의 빠르기를 갖습니다.
한편 제니는 버스의 양옆으로부터 5.0 m씩 떨어진 버스의 중앙에 서있어요.
그곳에서 버스가 진행하는 방향으로 파랑색 레이저를, 그 반대방향으로 자주색 레이저를 동시에 발사했다고 생각해봐요.
그러면 제니 J의 입장에서 파랑색 레이저 L의 상대 속도는 v_{LJ}=1.0~c로서 빛의 속도로 날아갑니다.
또한 자주색 레이저도 빠르기는 빛의 속도와 같으나 진행 방향이 파랑색 레이저와 반대 방향입니다. 그래서 자주색 레이저의 상대 속도에는 음수가 부여되어 있어요.
1-1. 제니의 관점
제니의 관점에서 두 레이저는 동일한 빛의 빠르기로 동일한 거리 5.0 m를 서로 반대방향으로 이동하므로 레이저는 동일한 순간에 버스의 앞쪽과 뒤쪽 면에 동시에 도달하게 됩니다.
동시에 도달하기 까지 걸린 시간을 수치적으로 구하면 다음과 같아요. 등속도 운동방정식을 사용하면 됩니다.
\tag{1}
\begin{align}
t = {s \over v_{LJ}} &= {{5.0~ \mathrm m}\over{1.0~c}} \\
&={{5.0~\mathrm{m}}\over{1.0 \times (3.0\times 10^8~\mathrm{m/s})}} \\
&= 16.67 \times 10^{-9}~\mathrm{s} \\
&= 16.67 ~\mathrm{ns}
\end{align}(1)식의 가장 마지막 줄에 ns가 쓰여져 있는데 이것은 ‘나노초’를 의미합니다. 초는 단위이고 나노는 10^{-9}의 크기를 뜻하는 단위앞에 붙는 접두어입니다.
제니의 입장에서 파랑색과 자주색 레이저는 각각 16.67 ns가 경과할 때 버스의 앞쪽과 뒤쪽 면에 동시에 도달합니다.
이것은 제니가 레이저 포인터 두개를 동시에 켰기 때문입니다.
1-2. 케빈의 관점
그렇다면 이번에는 제니가 레이저 포인터를 켜고 레이저가 발사되는 모습을 버스 밖에 있는 케빈이 관찰하고 있다고 가정해 보세요.
케빈이 관찰한 파랑색 레이저의 속도 \color{blue} v_{LK}는 갈릴레이 덧셈 규칙을 적용하여 다음 관계식으로 구할 수 있어요.(지금부터 속도 기호의 색상으로 파랑색 레이저와 자주색 레이저의 속도를 구분하겠습니다.)
\tag{2}
\begin{align}
\color{blue}v_{LK} &= v_{LJ} + v_{JK}\\
&=1.0 ~c + 0.5~c\\
&=1.5~c
\end{align}같은 방식으로 케빈이 관찰한 자주색 레이저의 속도 \color{magenta}v_{LK}는 다음과 같아요.
\tag{3}
\begin{align}
\color{magenta}v_{LK} &= v_{LJ} + v_{JK}\\
&=-1.0 ~c + 0.5~c\\
&=-0.5~c
\end{align}결국 케빈이 관찰하는 파랑색 레이저의 속도는 빛의 속도인 광속에 버스의 속도가 더해져 1.5~c가 되며, 자주색 레이저의 속도는 광속에 버스의 속도가 빠져 -0.5~c가 됩니다.
여기서 음수는 방향이 반대임을 뜻한다는 것 기억하세요.
그렇다면 케빈이 관찰할 때 두 레이저는 동시에 버스의 앞면과 뒷면에 도달할 까요? 각 레이저가 앞면과 뒷면에 도달하는데 걸리는 시간을 구해보면 알 수 있을거에요.
이것을 계산하기 위해서는 레이저가 이동하는 동안 버스도 이동중임을 꼭 계산에 포함시켜야 해요.
우선 파랑색 레이저가 버스 앞면에 도달하는 시간을 구해보겠습니다.
케빈이 관찰한 파랑색 레이저의 속도 \color{blue} v_{LK}는 1.5~c이므로 어느 시간 t_1동안 이동한 거리는 x_1 = \color{blue} v_{LK} \color{black} \times t_1으로 주어집니다.
한편 버스는 앞쪽으로 계속 이동중이므로 레이저가 버스의 앞면으로 다가가는 동안 버스의 앞면도 앞으로 계속 진행합니다.
그래서 시간 t_1동안 버스의 앞면이 이동한 거리 x_2 = x_0 + (v_{JK} \times t_1 )이 됩니다. 여기서 x_0는 [그림 1]에서 제니를 기준으로 버스 앞면까지의 거리 5.0 m를 의미합니다.
결국 제니가 발사한 파랑색 레이저가 버스의 앞면에 도달하기 위해서는 x_1과 x_2가 같아야 한다는 조건이 성립합니다.
\tag{4}
\begin{align}
x_1 &= x_2\\
\color{blue} v_{LK} \color{black} \times t_1 &= x_0 + (v_{JK} \times t_1 )\\
1.5 ~c \times t_1 &=5.0~\mathrm{m} + (0.5~c \times t_1)\\
\end{align}이제 도달 시간 t_1을 구하면 다음과 같아요.
\tag{5}
\begin{align}
t_1 & = {{5.0~\mathrm{m}}\over{1.0~c}}\\
&={{5.0~\mathrm{m}}\over{1.0 \times (3.0\times 10^8~\mathrm{m/s})}} \\
&= 16.67 \times 10^{-9}~\mathrm{s} \\
&= 16.67 ~\mathrm{ns}
\end{align}같은 방식으로 자주색 레이저가 버스의 뒷면에 도달하는 시간 t_2는 아래와 같이 구할 수 있어요. 이때 x_0는 제니보다 뒤쪽에 있으므로 -5.0 m가 적용됩니다.
\tag{6}
\begin{align}
x_1 &= x_2\\
\color{magenta} v_{LK} \color{black} \times t_2 &= x_0 + (v_{JK} \times t_2 )\\
-0.5 ~c \times t_2 &=-5.0~\mathrm{m} + (0.5~c \times t_2)\\
\end{align}이제 도달 시간 t_2를 구하면 다음과 같아요.
\tag{7}
\begin{align}
t_2 & = {{-5.0~\mathrm{m}}\over{-1.0~c}}\\
&={{-5.0~\mathrm{m}}\over{-1.0 \times (3.0\times 10^8~\mathrm{m/s})}} \\
&=16.67 \times 10^{-9}~\mathrm s \\
&= 16.67 ~\mathrm{ns}
\end{align}신기하게도 (5)식과 (7)식의 최종값은 16.67 ns가 동일하게 도출되었어요.
이것은 케빈이 관찰할 때 파랑색과 자주색 레이저는 동일한 순간에 버스의 앞면과 뒷면에 도달한다는 의미에요. 또한 16.67 ns는 (1)식으로 구한 제니 관점에서의 시간과 동일하다는 것도 알 수 있어요.
이것은 뉴턴 역학을 적용하면 어느 관성기준계에서 동시에 일어난 사건은 다른 관성기준계에서 관찰할 때에도 동시에 일어난사건으로 볼수 있다는 것을 의미합니다. 즉 시간은 모든 관성기준계에서 동일하다는 것을 뜻합니다.
이 결과는 우리의 상식과 일치합니다.
하지만 아인슈타인이 특수 상대성 이론을 만들면서 이러한 상식은 깨지게 됩니다. 즉 뉴턴역학의 한계가 드러나게 되죠.
바로 ‘동시성의 상대성’ 개념이 등장하게 됩니다. 더 알아보겠습니다.
2. 동시성의 상대성
아인슈타인은 특수 상대성 이론을 만들면서 상대성 원리와 광속 불변의 법칙이라는 중요한 가정을 하게 됩니다.
여기서 가정이라는 표현은 일단 이것이 옳다고 설정하고 이론을 전개했다는 의미에요.
그중 광속 불변의 법칙은 “진공중에서 빛의 속력은 모든 관성기준계에서 동일하며 광원의 운동과도 관련이 없다”라는 표현입니다.
이것을 더 쉽게 말씀드리면 등속으로 움직이는 어느 관성기준계에서 관찰한 빛의 속력을 c라고 할때, 이 빛을 정지한 관성기준계에서 관찰하더라도 c가 성립한다는 거에요.
이것은 갈릴레이 변환과 아주 큰 차이가 있는거에요.
위에서 설명드렸듯이 갈릴레이 변환에서는 앞쪽으로 움직이는 버스에서 앞쪽으로 발사한 빛은 c가 맞는데요. 이 빛을 정지한 관성기준계에서 관찰하면 빛의 속도는 버스의 이동속도를 더해 주어야 합니다.
결국 정지한 관찰자가 측정한 빛의 속도는 광속 c보다 커지는 것이 자연스러운 거였어요..
그런데 광속 불변의 법칙에 의하면 어느 관성계에서 관측하더라도 빛의 속도는 항상 c가 되어야 한다고 하니 신기할 뿐입니다.
아무튼 광속불변의 법칙을 반영하여 [그림 1]의 상황을 다시 해석해 보겠습니다.
[그림 1]이 저 위에 있으니 보기가 불편하잖아요. 아래에 [그림 2]로 다시 보여드리겠습니다.
![[그림 2] 동시성의 상대성. 제니가 오른쪽으로 등속으로 움직이는 버스안의 중간에 서 있습니다. 그리고 광속 <span class="katex-eq" data-katex-display="false">c</span>인 레이저를 왼쪽과 오른쪽으로 5 m 떨어진 벽을 향해 동시에 발사했어요. 그리고 그 레이저를 버스 밖에 있는 케빈이 관찰하고 있습니다. 광속 불변의 법칙에 의하면 케빈이 관찰한 파랑색 레이저의 속도는 광속 <span class="katex-eq" data-katex-display="false">c</span>이고, 자주색 레이저도 광속 <span class="katex-eq" data-katex-display="false">c</span>가 되어야 합니다.](https://ballpen.blog/wp-content/uploads/2023/03/갈릴레이-변환1-1024x548.jpg)
2-1. 제니의 관점
제니는 버스 안에서 오른쪽과 왼쪽 방향을 향해 파랑색과 자주색 레이저를 동시에 발사했어요. 이때 버스는 등속으로 움직이는 관성기준계이므로 제니가 관찰한 레이저 빛의 속도는 광속 c가 되어야 합니다.
결국 두 레이저가 버스의 앞면과 뒷면에 도달하는 시간은 (1)식에서와 같이 16.67 ns가 되어야 해요.
\tag{8}
t=16.67~\mathrm{ns}결국 동일한 순간에 버스의 앞면과 뒷면에 레이저가 도달하는 것은 당연합니다. 왜냐면 제니가 레이저를 동시에 발사했으니까요.
2-2. 케빈의 관점
이번에는 케빈의 관점에서 레이저가 버스의 앞면과 뒷면에 도달하는 시간을 구해보겠습니다. 물론 아인슈타인의 광속 불변의 법칙을 적용합니다.
그러면 케빈이 관찰한 파랑색과 자주색 레이저의 속도는 (2)식과 (3)식처럼 버스의 이동속도에 의해 달라지지 않아요. 믿기 어렵겠지만 케빈이 관찰하는 파랑색과 자주색 레이저의 빠르기는 모두 c입니다.
다만 자주색 레이저는 파랑색 레이저의 진행방향과 반대라는 측면에서 음수가 붙습니다.
\tag{9}
\color{blue} v_{LK} \color{black}= 1.0~c\tag{10}
\color{magenta} v_{LK} \color{black} = -1.0 ~c그럼 파랑색 레이저가 버스의 앞면에 도달하는 시간을 구해보겠습니다. (4)식과 동일한 방법으로 풀이하면 되는데요. 다만 \color{blue}v_{LK} \color{black}=1.0~c를 적용해야 해요.
\tag{11}
\begin{align}
x_1 &= x_2\\
\color{blue} v_{LK} \color{black} \times t_1 &= x_0 + (v_{JK} \times t_1 )\\
1.0 ~c \times t_1 &=5.0~\mathrm{m} + (0.5~c \times t_1)\\
\end{align}이제 도달 시간 t_1을 구하면 다음과 같아요.
\tag{12}
\begin{align}
t_1 & = {{5.0~\mathrm{m}}\over{0.5~c}}\\
&={{5.0~\mathrm{m}}\over{0.5 \times (3.0\times 10^8~\mathrm{m/s})}} \\
&= 33.33 \times 10^{-9}~\mathrm{s} \\
&= 33.33 ~\mathrm{ns}
\end{align}같은 방식으로 자주색 레이저가 버스의 뒷면에 도달하는 시간 t_2는 아래와 같이 구할 수 있어요. 이때 x_0는 제니보다 뒤쪽에 있으므로 -5.0 m가 적용됩니다.
\tag{13}
\begin{align}
x_1 &= x_2\\
\color{magenta} v_{LK} \color{black} \times t_2 &= x_0 + (v_{JK} \times t_2 )\\
-1.0 ~c \times t_2 &=-5.0~\mathrm{m} + (0.5~c \times t_2)\\
\end{align}이제 도달 시간 t_2를 구하면 다음과 같아요.
\tag{14}
\begin{align}
t_2 & = {{-5.0~\mathrm{m}}\over{-1.5~c}}\\
&={{-5.0~\mathrm{m}}\over{-1.5 \times (3.0\times 10^8~\mathrm{m/s})}} \\
&= 11.11 \times 10^{-9}~\mathrm{s} \\
&= 11.11 ~\mathrm{ns}
\end{align}결과가 어떻게 주어졌나요? 파랑색 레이저가 앞면에 도달하는데 걸리는 시간은 33.33 ns이고 자주색 레이저가 뒷면에 도달하는 시간은 11.11 ns로 계산되었습니다.
이것이 뜻하는 것은 케빈의 관점에서 파랑색 레이저에 비해 자주색 레이저가 더 빨리 뒷면에 도달한다는 것을 의미해요. 그러므로 케빈은 제니가 레이저 포인터를 동시에 켠 것이 아닌 자주색 레이저 포인터를 먼저 켜고 나중에 파랑색 레이저 포인터를 켰다고 믿게 됩니다.
제니는 두 레이저 포인터를 동시에 분명히 켰는데, 케빈은 동시에 켠 것이 아니라는 주장을 하게 됩니다.
이와 같이 어느 관성기준계에서 동시에 일어난 사건이 다른 관성기준계에서 관찰하면 동시에 일어난 사건이 아닐 수 있습니다. 바로 이것을 ‘동시성의 상대성’이라 합니다.
3. 동시성의 상대성 개념 요약
자 이제 정리해보겠습니다.
갈릴레이 변환을 기본으로 하는 뉴턴역학에 따르면 어느 한 관성기준계에서 동시에 일어난 사건은 다른 관성기준계에서 관찰하더라도 동시에 일어난 사건입니다.
또한 갈릴레이 변환에 따르면 빛의 속도는 광속보다 더 빨라질 수도 있어요.
그러나 아인슈타인의 광속 불변의 법칙을 반영하면 어느 한 관성기준계에서 동시에 일어난 사건은 다른 관성기준계에서 관찰할 때 동시에 일어난 사건으로 보이지 않아요. 바로 이것을 동시성의 상대성이라 합니다.
그리고 광속 불변의 법칙에 따라 빛의 속도는 어느 관성기준계에서 관찰하더라도 광속 c보다 빨라질 수 없어요.
그렇다면 과연 갈릴레이 변환이 틀리고 광속 불변의 법칙이 맞느냐에 대한 의심이 들 수 있는데요. 실험적 사실을 기반으로 할 때 광속 불변의 법칙이 맞습니다.
이에 대해서는 어느 관성기준계가 아주 빠르게 움질일 때 시간 지연과 길이 수축 현상에 대한 이야기로 이어집니다.