속박전하 예제 - ilovemyage

BallPen · 2025-01-14T22:17:43+09:00

속박전하 예제 하나를 풀어보겠습니다. 균일하게 편극된 구에 의한 전위와 전기장을 구하는 문제입니다. 편극된 구 내부의 전기장은 편극밀도와 반대방향을 갖는 상수벡터로 주어지며, 구 외부의 전기장은 전기쌍극자에 의한 전기장과 동일하다는 것을 알 수 있습니다.

Last Updated on 2025-01-15 by BallPen

속박전하에 의한 전압과 전기장을 구해 봐요.

속박전하 예제 하나를 풀어 봐요. 아래는 이번 글의 목차입니다.

Contents

1. 속박전하 예제
2. 편극된 구의 속박 전하 밀도
3. 편극된 구에 의한 전위
- 3-1. 구 내부의 전위
- 3-2. 구 외부의 전위
4. 편극된 구에 의한 전기장
- 4-1. 구 내부의 전기장
- 4-2. 구 외부의 전기장

이 글에서 사용된 그림은 키노트로 작성되었습니다. 그림파일이 필요한 분은 다운받아 사용하세요. bound_charges_example.key

1. 속박전하 예제

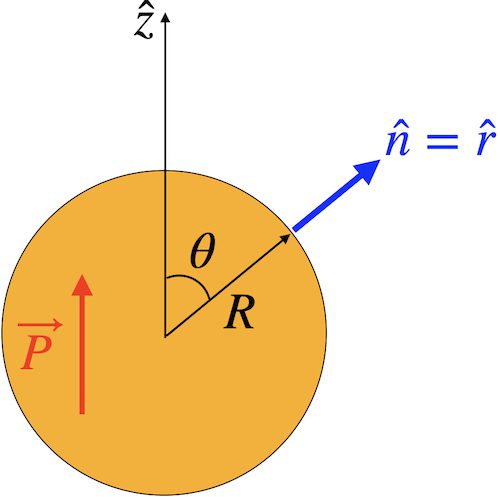
아래 그림과 같이 $\vec P = P \hat z$ 로 균일하게 편극된 반지름 $R$ 인 구에 의한 전위와 전기장을 구해 보세요.

2. 편극된 구의 속박 전하 밀도

속박전하에 대한 글에서 설명드렸듯이 편극밀도의 발산 $-\nabla \cdot \vec P$ 은 체적 속박 전하 밀도 $\rho_b$ 입니다.

\tag{1} \rho_b =- \nabla \cdot \vec P

그런데 문제에서 $\vec P$ 가 구 내부에서 균일하다고 하였으므로 편극밀도의 발산은 0이 될거에요. 왜냐면 상수벡터를 미분하면 0이 되기 때문이죠. 이는 결국 체적 속박 전하 밀도 $\rho_b = 0$ 임을 알 수 있어요.

반면에 표면 속박 전하 밀도는 다음 식과 같이 주어집니다.

\tag{2} \sigma_b = \vec P \cdot \hat n

그러므로 편극밀도 $\vec P$ 와 유전체 표면의 미소 면벡터 $\hat n$ 사이의 스칼라 곱에 따라 표면 속박 전하 밀도의 크기와 분포가 결정될 것임을 예상할 수 있어요.

3. 편극된 구에 의한 전위

문제에서 주어진 균일한 편극밀도 $\vec P$ 는 결국 표면 속박 전하 밀도 때문에 만들어진 것임을 알게 되었어요.

구의 중심을 원점으로 설정하고 그 중심에서 $r$ 만큼 떨어진 곳에서의 편극된 물체에 의한 전위는 다음과 같이 주어집니다.

\tag{3} V(\vec r) = {1 \over{4 \pi \epsilon_0}} \int {{\vec P \cdot \hat r}\over{r^2}} d \tau^{\prime}

한편 편극밀도는 상수이므로 적분 기호 밖으로 빼내어 정리할게요.

\tag{4} V(\vec r) = \vec P \cdot {1 \over{4 \pi \epsilon_0}} \int {{\hat r}\over{r^2}} d \tau^{\prime}

윗 식의 $d \tau^{\prime}$ 에 구면좌표계에서의 미소 부피 요소를 대입해서 적분하면 되는데요.

이때 $r<R$ 인 구 내부에서의 전위와 $r \geq R$ 인 구 외부에서의 전위로 구분해서 풀어볼게요.

3-1. 구 내부의 전위

구 내부의 전위 $V_{in}$ 을 구하기 위해서는 다음과 같이 하면 됩니다. 이때 $r^{\prime}$ 의 적분 구간은 0에서 $r$ 까지로 하면 되죠.

\tag{5} \begin{align} V_{in} &= \vec P \cdot {1 \over{4 \pi \epsilon_0}} \int {{\hat r}\over{r^2}} d \tau^{\prime} \\[10pt] &=\vec P \cdot {1 \over{4 \pi \epsilon_0}} \int_0^{2 \pi} \int_0^{\pi} \int_0^r {{\hat r}\over{r^2}} {r^{\prime}}^2 dr^{\prime} \sin \theta d\theta d \phi\\[10pt] &=\vec P \cdot {1\over{4 \pi \epsilon_0}} \int_0^{2 \pi} \int_0^{\pi} \Big[ {{\hat r}\over{r^2} }{{{r^{\prime}}^3}\over{3}}\Big]_0^r \sin \theta d \theta d \phi\\[10pt] &=\vec P \cdot {1 \over{4 \pi \epsilon_0}} \int_0^{2 \pi} \int_0^{\pi} {{r \hat r}\over{3}} \sin \theta d\theta d \phi\\[10pt] &=\vec P \cdot \Big( {1 \over{4 \pi \epsilon_0}}\Big) \Big( {{r \hat r}\over{3}} \Big) \int_0^{2 \pi} \Big[ -\cos \theta\Big]_0^{\pi} d \phi\\[10pt] &=\vec P \cdot \Big( {1 \over{4 \pi \epsilon_0}}\Big) \Big( {{r \hat r}\over{3}} \Big)\int_0^{2\pi} 2 d\phi\\[10pt] &=\vec P \cdot \Big( {1 \over{4 \pi \epsilon_0}}\Big) \Big( {{r \hat r}\over{3}} \Big)\Big(2\Big) \Big[\phi \Big]_0^{2\pi} \\[10pt] &=\vec P \cdot \Big( {1 \over{{\cancel{4 \pi}} \epsilon_0}}\Big) \Big( {{r \hat r}\over{3}} \Big)\Big({\cancel{4 \pi}}\Big) \\[10pt] &={{\vec P \cdot \vec r}\over{3 \epsilon_0}}\\[10pt] &={{Pr \cos \theta}\over{3 \epsilon_0}} \end{align}

3-2. 구 외부의 전위

구 외부의 전위 $V_{out}$ 을 구하기 위해서는 다음과 같이 하면 됩니다. 다만 $r^{\prime}$ 의 적분 구간은 0에서 $R$ 까지로 제한되겠죠.

\tag{6} \begin{align} V_{out} &= \vec P \cdot {1 \over{4 \pi \epsilon_0}} \int {{\hat r}\over{r^2}} d \tau^{\prime} \\[10pt] &=\vec P \cdot {1 \over{4 \pi \epsilon_0}} \int_0^{2 \pi} \int_0^{\pi} \int_0^R {{\hat r}\over{r^2}} {r^{\prime}}^2 dr^{\prime} \sin \theta d\theta d \phi\\[10pt] &=\vec P \cdot {1\over{4 \pi \epsilon_0}} \int_0^{2 \pi} \int_0^{\pi} \Big[ {{\hat r}\over{r^2} }{{{r^{\prime}}^3}\over{3}}\Big]_0^R \sin \theta d \theta d \phi\\[10pt] &=\vec P \cdot {1 \over{4 \pi \epsilon_0}} \int_0^{2 \pi} \int_0^{\pi} {{R^3 \hat r}\over{3r^2}} \sin \theta d\theta d \phi\\[10pt] &=\vec P \cdot \Big( {1 \over{4 \pi \epsilon_0}}\Big) \Big( {{R^3 \hat r}\over{3r^2}} \Big) \int_0^{2 \pi} \Big[ -\cos \theta\Big]_0^{\pi} d \phi\\[10pt] &=\vec P \cdot \Big( {1 \over{4 \pi \epsilon_0}}\Big) \Big( {{R^3 \hat r}\over{3r^2}} \Big)\int_0^{2\pi} 2 d\phi\\[10pt] &=\vec P \cdot \Big( {1 \over{4 \pi \epsilon_0}}\Big) \Big( {{R^3 \hat r}\over{3r^2}} \Big)\Big(2\Big) \Big[\phi \Big]_0^{2\pi} \\[10pt] &=\vec P \cdot \Big( {1 \over{{\cancel{4 \pi}} \epsilon_0}}\Big) \Big( {{R^3 \hat r}\over{3r^2}} \Big)\Big({\cancel{4 \pi}}\Big) \\[10pt] &={{\vec P \cdot R^3 \hat r}\over{3 \epsilon_0 r^2}}\\[10pt] &={{PR^3 \cos \theta}\over{3 \epsilon_0 r^2}} \end{align}

4. 편극된 구에 의한 전기장

그럼 이번에는 편극된 구가 만드는 전기장을 구해 봐요.

위에서 구한 전위 $V_{in}$ 과 $V_{out}$ 에 기울기 연산을 함으로써 구 안과 밖의 전기장을 구할 수 있어요.

4-1. 구 내부의 전기장

구 내부의 전위 $V_{in}$ 을 나타내는 (5)식에 구면좌표계에서의 기울기 연산을 한 후 마이너스 부호를 붙여주면 됩니다.

\tag{7} \begin{align} \vec E_{in} &= - \nabla V_{in} \\[10pt] &=-\nabla\Big( {{Pr \cos \theta}\over{3 \epsilon_0}}\Big)\\[10pt] &=-\Big( {{\partial}\over{\partial r}} \hat r + {1 \over r} {{\partial}\over{\partial \theta}} \hat \theta\Big)\Big( {{Pr \cos \theta}\over{3 \epsilon_0}}\Big)\\[10pt] &=-{{P \cos \theta}\over{3 \epsilon_0}}\hat r +{{P \sin \theta}\over{3 \epsilon_0}} \hat \theta\\[10pt] &=-{{P}\over{3 \epsilon_0}}{\color{blue}(\cos \theta \hat r - \sin \theta \hat \theta)} \end{align}

이때 윗 식에서 파랑색 부분의 벡터가 나오게 되는데요. 이 벡터는 [그림 1]에서 $z$ 방향의 단위벡터 $\hat z$ 와 같습니다.

이를 반영하면 (7)식의 마지막 줄은 다음과 같아요.

\tag{8} \vec E_{in} = - {{P}\over{3 \epsilon_0}}\hat z

결국 균일하게 편극된 구 내부의 전기장 $\vec E_{in}$ 은 편극밀도 $P \hat z$ 와 반대방향을 갖는 상수 벡터로 주어짐을 알 수 있습니다.

4-2. 구 외부의 전기장

이번에는 구 외부의 전기장을 구해 봐요. (6)식의 $V_{out}$ 을 활용하면 됩니다.

\tag{9} \begin{align} \vec E_{out} &= - \nabla V_{out} \\[10pt] &=-\nabla\Big( {{PR^3 \cos \theta}\over{3 \epsilon_0 r^2}}\Big)\\[10pt] &=-\Big( {{\partial}\over{\partial r}} \hat r + {1 \over r} {{\partial}\over{\partial \theta}} \hat \theta\Big)\Big( {{PR^3 \cos \theta}\over{3 \epsilon_0 r^2}}\Big)\\[10pt] &={{2PR^3 \cos \theta}\over{3 \epsilon_0 r^3}}\hat r +{{PR^3 \sin \theta}\over{3 \epsilon_0 r^3}} \hat \theta\\[10pt] \end{align}

한편 윗 식에서 편극밀도의 크기 $P$ 는 단위부피당 그 부피에 있는 총 쌍극자모멘트의 합으로 정의되므로 다음과 같이 표현할 수 있습니다.

\tag{10} P = {{p}\over{{4}\over{3}}\pi R^3}

그리고 (10)식을 (9)식에 대입하세요. 그리고 정리하면 다음과 같습니다.

\tag{11} \begin{align} \vec E_{out} &={{2PR^3 \cos \theta}\over{3 \epsilon_0 r^3}}\hat r +{{PR^3 \sin \theta}\over{3 \epsilon_0 r^3}} \hat \theta\\[10pt] &= {1 \over{4 \pi \epsilon_0 r^3}} (2 p \cos \theta \hat r + p \sin \theta \hat \theta) \end{align}

위 (11)식이 구 외부의 전기장을 나타내는 식입니다.

그런데 이 식의 물리적 의미를 더 살펴보기 위해 살짝만 식의 형태를 바꾸어 볼게요.

이를 위해 구면좌표계의 단위벡터 $\hat r$ 과 $\hat \theta$ 을 아래와 같이 대입해서 정리해 보세요. 그러면 다음과 같습니다.

\tag{12} \begin{align} \vec E_{out} &= {1 \over{4 \pi \epsilon_0 r^3}} (2 p \cos \theta \hat r + p \sin \theta \hat \theta)\\[10pt] &={1 \over{4 \pi \epsilon_0} r^3} \Big[2p\cos \theta (\sin \theta \cos \phi \hat x +\sin \theta \sin \phi \hat y + \cos \theta \hat z)\\[10pt] &~~~~~~~~~~~~+p \sin \theta (\cos \theta \cos \phi \hat x + \cos \theta \sin \phi \hat y - \sin \theta \hat z)\Big]\\[10pt] &={{1}\over{4 \pi \epsilon_0}r^3}\Big[3 p \cos \theta (\sin \theta \cos \phi \hat x + \sin \theta \sin \phi \hat y )+p (2 \cos^2 \theta - \sin ^2 \theta)\hat z \Big]\\[10pt] &={1 \over{4 \pi \epsilon_0}r^3} \Big[ 3 p \cos \theta (\sin \theta \cos \phi \hat x + \sin \theta \sin \phi \hat y +{\color{red}{\cos \theta \hat z}}) {\color{red}{-3p \cos^2 \theta \hat z}}\\[10pt] &~~~~~~~~~~~~+p (2 \cos^2 \theta - \sin ^2 \theta)\hat z \Big]\\[10pt] &={1\over{4 \pi \epsilon_0}r^3} \Big[ 3p \cos \theta \hat r - 3p\cos^2 \theta \hat z + 2p \cos^2 \theta \hat z- p \sin^2 \theta \hat z \Big]\\[10pt] &={1 \over{4 \pi \epsilon_0}r^3} \Big[ 3p \cos \theta \hat r - p (\cos^2 \theta + \sin^2 \theta) \hat z \Big]\\[10pt] &={1 \over{4 \pi \epsilon_0}r^3} \Big[3 {\color{blue}p \cos \theta} \hat r- p \hat z \Big] \end{align}

위 식에서 빨강색 부분은 식을 정리하기 위해 동일한 양을 더해주고 빼준 것입니다. 또한 파랑색 부분은 $p\cos \theta$ 은 $\vec p \cdot \hat r$ 으로 바꾸어 표현할 수 있어요.

그래서 (12)식의 마지막 줄은 다음과 같이 다시 쓸 수 있습니다.

\tag{13} \begin{align} \vec E_{out}={1 \over{4 \pi \epsilon_0}r^3}\Big[3(\vec p \cdot \hat r) \hat r - \vec p\Big] \end{align}

어떤가요? 어디서 보았던 것처럼 익숙한 식인가요?

바로 (13)식은 전기쌍극자가 만드는 전기장과 식의 모양이 같다는 것을 알 수 있어요.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]