시정수 (time constant)

BallPen · 2023-05-16T22:01:57+09:00

시정수(time constant)는 지수함수적으로 변하는 어떤 양이 있을 때 최종값에 도달하는 시간을 비교하기 위한 척도입니다. 보통 시정수의 5배의 시간이 지나면 최종값에 도달한 것으로 간주합니다. 시상수, 시간정수, 특성시간 등으로 불리기도 합니다.

Last Updated on 2023-05-16 by BallPen

시정수를 정의하는 이유와 활용 사례를 소개합니다.

시정수 (time constant)란 지수함수적으로 변하는 어떤 양이 최종값에 도달하는데 걸리는 시간을 나타내는 척도입니다. 때로 시정수를 시상수, 시간상수, 특성시간이라고도 부릅니다.

이번 글에서는 시정수를 정의하는 이유와 시정수가 활용되는 몇가지 사례를 소개합니다. 생각보다 어렵지 않고 상당히 유용한 개념이에요.

함께 시작해 봐요.

아래는 이번 글의 목차입니다.

Contents

1. 지수함수적 변화
- 1-1. RC 회로에서 축전기가 충전될 때 전류 변화
- 1-2. RL 회로에서 인덕터의 역기전력에 의한 전류변화
2. 시정수 정의하는 이유
- 2-1. RC 회로에서의 전류 변화
- 2-2. RL 회로에서의 전류 변화

1. 지수함수적 변화

어떤 양이 지수함수적으로 변하는 경우가 있어요.

예를 들어 저항과 축전기로 구성된 RC 회로에서 축전기가 충전되거나 방전되는 경우 회로를 통과하는 전류는 지수함수적으로 변합니다. 또 하나의 예로는 등속으로 움직이는 물체에 유체저항력이 작용할때 물체의 속도도 지수함수적으로 변해요.

시정수는 이와 같이 지수함수적으로 변하는 어떤 양을 기술할 때 그 개념이 활용됩니다.

시정수가 어떻게 정의되는지 몇가지 사례를 알아보겠습니다.

1-1. RC 회로에서 축전기가 충전될 때 전류 변화

저항과 축전기가 직렬 연결된 회로를 RC 회로라고 합니다.

이 회로에 직류전원이 연결되면 회로에 전류가 흐르며 축전기가 충전되는데요. RC 회로에서 축전기의 충전과정에 회로를 통과하는 전류 $i$ 는 시간 $t$ 의 함수로써 다음과 같이 주어집니다.

\tag{1} i=I_0 e^{-{t \over RC}}

여기서 $I_0$ 는 초기 전류이고, $R$ 은 저항값, $C$ 는 축전기의 전기용량을 뜻합니다.

(1)식에 따르면 축전기가 충전될수록 전류 $i$ 는 시간의 함수로써 지수함수적으로 변하며 0으로 가까워지는데요. 이때 지수항의 분모에 있는 $RC$ 를 시정수 $\tau$ 로 정의합니다.

시정수를 반영해서 (1)식을 다시 쓰면 다음과 같아요.

\tag{2} \tau = RC

\tag{3} i=I_0 e^{-{t \over \tau}}

그렇다면 (2)식에 정의된 시정수의 단위는 무엇일까요?

간단히 유추해 본다면 (3)식에서 $i$ 의 단위는 전류의 단위인 A이고, $I_0$ 의 단위도 A입니다. 그러므로 지수항은 단위가 없어야 해요. 만일 지수항에 단위가 있다면 좌변과 우변의 단위가 달라져 (3)식은 성립할 수 없어요.

결국 지수항의 단위가 사라지기 위해서는 지수항에 있는 시간 $t$ 의 단위인 s가 사라져야 하므로 시정수의 단위가 시간의 단위인 $s$ 가 되어야 한다는 논리가 성립합니다.

정말 시정수 $\tau$ 의 단위가 s가 되는지 유도해 보겠습니다.

\tag{4} \begin{align} \tau = RC ~~&\Big[\Omega\cdot \mathrm{F} = {\mathrm V \over \mathrm A} \cdot {\mathrm C \over \mathrm V} = {\mathrm C \over \mathrm A } = \mathrm s \Big] \end{align}

(4)식과 같이 $RC$ 로 정의된 시정수 $\tau$ 의 단위는 시간의 단위인 s가 됨을 알 수 있습니다.

그래서 시정수를 시간과 관련된 개념으로 시간 정수, 시간 상수, 특성 시간 등으로 불리게 되었어요.

그렇다면 시정수는 굳이 왜 정의하는 걸까요? 이에 대해서는 별도로 아래에서 따로 설명드리겠습니다. 우선 시정수가 정의되는 다른 사례를 또 하나 알아봐요.

1-2. RL 회로에서 인덕터의 역기전력에 의한 전류변화

저항 $R$ 과 인덕터 $L$ 이 직렬 연결된 회로를 RL 회로라고 합니다.

이 회로에 기전력 $V$ 가 연결되면 전류가 흐르게 되는데요. 시간의 함수로써 전류의 변화를 나타내면 다음 (5)식과 같습니다.

\tag{5} i = {V \over R} (1-e^{- {R \over L}t})

이때 $L/R$ 을 시정수 $\tau$ 라고 정의한다면 (5)식은 다음과 같습니다.

\tag{6} \begin{align} \tau = {L \over R} \end{align}

\tag{7} i = {V \over R} (1- e^{-{t \over \tau}})

한편 지수항의 단위가 없어야 (7)식의 양변이 전류의 단위 A로 서로 같아집니다. 결국 (6)식으로 주어진 시정수 $\tau$ 의 단위는 시간의 단위인 s가 되어야 합니다.

이를 직접 구해보면 다음과 같습니다.

\tag{8} \begin{align} \tau = {L \over R} ~~&\Big[ \mathrm{{{V \cdot s/A}\over{V/A}}} = \mathrm{s} \Big] \end{align}

결국 $L/R$ 의 단위도 시간의 단위인 s로 주어짐을 알 수 있어요.

그렇다면 이제부터 시정수를 정의하는 이유를 알아보겠습니다.

2. 시정수 정의하는 이유

시정수를 정의하는 이유는 지수함수적으로 변하는 어떤 양이 최종값에 도달하는데 걸리는 시간을 비교하기 위한 것입니다. 이때 최종값에 도달하는 시간은 시정수의 5배로 간주합니다.

RC 회로와 RL 회로에서 회로를 지나가는 전류의 사례를 소개합니다.

2-1. RC 회로에서의 전류 변화

(3)식에서 $I_0$ 를 1.0 A라고 가정하겠습니다. 한편 저항 $R$ 을 2.2 k $\Omega$ , 축전기의 전기용량 $C$ 를 $0.1 \mu F$ 이라고 했을 때 시정수를 계산하면 아래와 같습니다.

\tag{9} \tau = RC = (2.2 \times 10^3 ~\Omega)(0.1 \times 10^{-6} \mathrm{F}) = 2.2\times 10^{-4} ~\mathrm{s}

한편 (3)식을 다시 정리하면 다음과 같이 쓸 수 있어요.

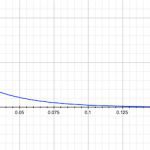
\tag{10} \begin{align} i&=I_0 e^{-{t \over \tau}}\\ &= (1.0~\mathrm{A})e^{-{{t}\over{\tau}}}\\ \end{align}

(10)식과 같이 전류 $i$ 는 1.0 A를 초기값으로 시작하여 지수함수적으로 감소하게 됩니다. 이것을 그래프로 나타낸 것이 [그림 1]의 빨강색 곡선입니다.

[그림 1] 시정수 기준으로 5배의 시간이 지나면 최종값에 도달한 것으로 간주됩니다.

이때 시간 $t$ 를 시정수 $\tau$ 의 정수배로 정한다면 (10)식의 전류는 다음과 같이 변할거에요.

\tag{11} \begin{align} &t=0 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{0\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{0}= 1.0~\mathrm{A}\\ &t=1 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{1\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{-1} = 0.37~\mathrm{A}\\ &t=2 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{2\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{-2} = 0.14~\mathrm{A}\\ &t=3 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{3\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{-3} = 0.050~\mathrm{A}\\ &t=4 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{4\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{-4} = 0.018~\mathrm{A}\\ &t=5 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{5\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{-5} = 0.0067~\mathrm{A}\\ \vdots\\ &t=10 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{10\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{-10} = 0.000045~\mathrm{A}\\ \vdots\\ &t=15 \tau~ 일때 \rightarrow i =(1.0~\mathrm{A} )e^{-{{15\tau}\over{\tau}}} =(1.0~\mathrm{A})\times e^{-15} = 0.00000031~\mathrm{A}\\ \vdots \end{align}

그런데 이때 중요한 것은 시간 $t$ 가 증가하여 축전기가 충전되면 회로에 흐르는 전류는 0에 가까워지기는 하지만 절대로 0이 되지 않는다는 거에요. 이것은 지수함수의 전형적인 특징입니다.

문제는 그렇다면 $RC$ 회로에서 축전기가 모두 100% 충전되기 위해서는 무수한 시간이 걸린다는 의미가 됩니다.

따라서 흐르는 전류가 수학적으로는 절대로 0이 될 수는 없지만 축전기가 모두 충전되어 전류가 0이 되었다고 간주할 수 있는 시간 기준을 정하면 좋을 것 같아요.

그래서 어떻게 정했냐면요.

시정수의 5배의 시간이 지나면 모두 충전된 것으로 간주합니다. 즉 $t = 5 \tau$ 의 시간이 지나면 축전기가 모두 충전되어 전류가 0이 된 것으로 봅니다. 이를 구체적으로 구해보면 다음과 같아요.

\tag{12} \begin{align} t &= 5 \tau \\ &= 5 \times (2.2\times10^{-4} ~\mathrm{s})\\ &= 0.0011 ~\mathrm {s} \end{align}

즉 시정수의 5배의 시간인 0.0011 s가 되면 RC 회로에 흐르는 전류는 이론적으로 (11)식에 따라 0.0067 A이지만 실질적으로 회로에 흐르는 전류는 0이 된것으로 간주합니다.

결국 시정수란 지수함수적으로 변하는 어떤 양이 있을 때 최종값(정상상태)에 도달하는 시간을 표현하는 하나의 대표값입니다.

그래서 시정수가 크면 최종값에 도달하는데 걸리는 시간이 길어지고, 시정수가 작으면 최종값에 도달하는데 걸리는 시간이 짧다는 의미를 갖습니다.

한편 1시정수, 즉 $1\tau$ 는 (11)식에서 알수 있는 것처럼 최종값의 $1/e$ 이 되는 시간입니다. 대략 최종값의 36.8%까지 변하는 시간이에요.

2-2. RL 회로에서의 전류 변화

(6)식과 (7)식에서 $V$ 를 10.0 V, $R$ 을 5.0 $\Omega$ , $L$ 을 $10.0~\mathrm{H}$ 라고 가정할 때 (6)식의 시정수를 계산하면 다음과 같습니다.

\tag{13} \begin{align} \tau &= {L \over R} = {{10.0~\mathrm{H}}\over{5.0~\mathrm{\Omega}}} = 2.0~\mathrm{s} \end{align}

한편 (7)식에 위에서 가정한 값들을 대입하면 다음과 같이 정리됩니다.

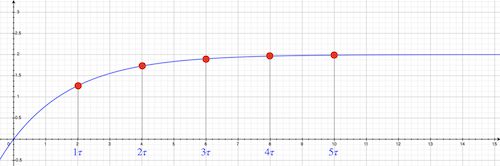
\tag{14} \begin{align} i &= {V \over R} (1- e^{-{t \over \tau}})\\[10pt] &={10.0~\mathrm{V} \over{5.0~\mathrm{\Omega}}}(1-e^{-{t \over \tau}})\\[10pt] &=(2.0~\mathrm{A}) (1-e^{-{t \over \tau}}) \end{align}

즉, 회로에 흐르는 전류 $i$ 는 아래 [그림 2]와 같이 0.0 A를 시작으로 지수함수적으로 증가한 후 2.0 A로 수렴하게 됩니다.

[그림 2] 시정수 기준으로 5배의 시간이 지나면 최종값에 도달한 것으로 간주합니다.

이때 시간 $t$ 를 시정수 $\tau$ 의 정수배로 정한다면 (14)식의 전류는 다음과 같이 변합니다.

\tag{15} \begin{align} &t=0\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{0 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^0) = 0\mathrm{A}\\ &t=1\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{1 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^{-1}) = 1.26\mathrm{A}\\ &t=2\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{2 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^{-2}) = 1.73\mathrm{A}\\ &t=3\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{3 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^{-3}) = 1.90\mathrm{A}\\ &t=4\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{4 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^{-4}) = 1.96\mathrm{A}\\ &t=5\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{5 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^{-5}) = 1.99\mathrm{A}\\ \vdots\\ &t=10\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{10 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^{-10}) = 1.999\mathrm{A}\\ \vdots\\ &t=15\tau~일때 \rightarrow i = (2.0~\mathrm{A})(1-e^{-{{15 \tau}\over {\tau}}}) = (2.0~\mathrm{A})\times(1-e^{-15}) = 1.999999\mathrm{A}\\ \vdots\\ \end{align}

여기서도 시간 $t$ 가 증가함에 따라 전류는 최종값인 2.0 A에 가까워지기는 하지만 절대로 2.0 A가 되지는 않아요.

따라서 이 경우에도 전류가 최종값에 도달하는데 무한히 긴 시간이 필요하다는 의미가 되므로, 최종값에 도달한 것으로 간주되는 시간을 정하면 좋을 것 같아요.

네 맞습니다.

바로 시정수의 5배의 시간이 지나면 최종값에 도달한 것으로 간주하면 좋을 것 같아요. 이를 구체적으로 구하면 다음과 같아요.

\tag{16} \begin{align} t &= 5 \tau\\ &= 5 \times (2.0~\mathrm{s})\\ &=10.0~\mathrm{s} \end{align}

즉, 10.0 s가 지나면 최종값에 도달한 것으로 간주합니다.

결국 시정수는 지수함수적으로 변하는 어떤 양이 최종값에 도달하는데 걸리는 시간을 비교하기 위한 하나의 척도로 볼 수 있습니다.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 4 Average: 4.3]

시정수 (time constant)