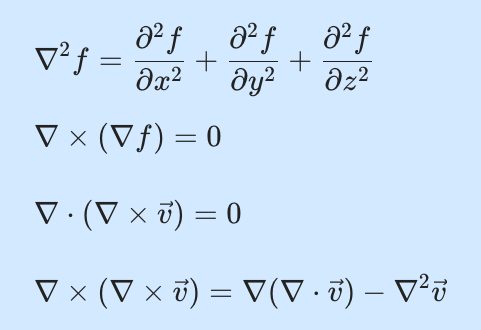Last Updated on 2025-09-07 by BallPen
벡터 미분 연산자를 이용한 이계 미분의 몇가지 곱셈 규칙을 알아봐요.
벡터 미분 연산자(또는 델연산자)를 활용한 이계 미분 곱셈 규칙 몇가지를 알아봅니다.
이 글을 통해 다음 곱셈규칙이 어떻게 성립하는지를 알 수 있어요.
\tag{D1}
\begin{aligned}
&\nabla^2 f = {{\partial^2 f}\over{\partial x^2}} + {{\partial^2 f}\over{\partial y^2}} + {{\partial^2 f}\over{\partial z^2}}\\[10pt]
&\nabla \times (\nabla f) =0\\[10pt]
&\nabla \cdot (\nabla \times \vec v) = 0\\[10pt]
&\nabla \times(\nabla \times \vec v) = \nabla(\nabla \cdot \vec v) - \nabla^2 \vec v
\end{aligned}하나씩 알아봐요.
Contents
1. 라플라시안(Laplacian)
어떤 스칼라함수 f에 대한 기울기의 발산(divergence of gradient)을 라플라시안이라고 합니다.
기호로 표현하면 \nabla \cdot (\nabla f)가 될텐데요. 통상적으로 간단하게 \nabla^2 f로 표현합니다.
벡터 미분 연산자 \nabla가 두번 사용되므로 이계 미분 곱셈규칙에 해당하죠.
구체적으로 라플라시안을 전개하면 다음과 같습니다.
\tag{1-1}
\begin{aligned}
\nabla ^2 f &= \nabla \cdot(\nabla f) \\[10pt]
&=\Big( {{\partial}\over{\partial x}} \hat x + {{\partial}\over{\partial y}} \hat y + {{\partial}\over{\partial z}} \hat z \Big) \cdot \Big( {{\partial f}\over{\partial x}} \hat x + {{\partial f}\over{\partial y}} \hat y + {{\partial f}\over{\partial z}} \hat z \Big) \\[10pt]
&={{\partial^2f}\over{\partial x^2}} {\color{blue}(\hat x \cdot \hat x)} + {{\partial^2 f}\over{\partial x \partial y}}{\color {red}(\hat x \cdot \hat y)} + {{\partial^2 f}\over{\partial x \partial z}}{\color{red}(\hat x \cdot \hat z)} \\[10pt]
&~~~~~~~+{{\partial^2 f}\over{\partial y \partial x}}{\color{red}(\hat y \cdot \hat x)} + {{\partial^2 f}\over{\partial y^2 }}{\color{blue}{(\hat y \cdot \hat y)}} + {{\partial^2 f}\over{\partial y \partial z}}{\color{red}(\hat y \cdot \hat z)} \\[10pt]
&~~~~~~~+ {{\partial^2 f}\over{\partial z \partial x}}{\color{red}(\hat z \cdot \hat x)} + {{\partial^2 f}\over{\partial z \partial y}} {\color{red}(\hat z \cdot \hat y)}+ {{\partial^2 f}\over{\partial z^2}}{\color {blue} (\hat z \cdot \hat z)} \\[10pt]
&={{\partial^2 f}\over{\partial x^2}}+{{\partial^2 f}\over{\partial y^2}}+{{\partial^2 f}\over{\partial z^2}}
\end{aligned}윗 식의 세번째 줄에 스칼라곱의 규칙을 적용하면 마지막 줄이 됩니다. 평행한 단위벡터 사이의 스칼라곱(파랑색 부분)은 1이되고, 수직한 단위벡터 사이의 스칼라곱(빨강색)은 0이 됩니다.
결국 어떤 스칼라함수에 대한 라플라시안은 다음과 같이 정의됩니다.
\tag{1-2}
\begin{align}
\nabla ^2 f &= \nabla \cdot(\nabla f) ={{\partial^2 f}\over{\partial x^2}}+{{\partial^2 f}\over{\partial y^2}}+{{\partial^2 f}\over{\partial z^2}}
\end{align}2. 기울기의 회전(Curl of a gradient)
어떤 스칼라함수 f에 대한 기울기의 회전(Curl of a gradient)은 항상 0이 되는데요.
이를 기호로 표현하면 \nabla \times (\nabla f)가 됩니다. 이를 전개해 볼게요. 정말 0이 되는지 확인해봐요.
\tag{2-1}
\begin{aligned}
\nabla \times (\nabla f) &= \nabla \times \Big({{\partial f}\over{\partial x}}\hat x + {{\partial f}\over{\partial y}}\hat y + {{\partial f}\over{\partial z}}\hat z \Big)\\[10pt]
&=
\begin{vmatrix}
\hat x & \hat y & \hat z\\[5pt]
{{\partial}\over{\partial x}} & {{\partial}\over{\partial y}} & {{\partial}\over{\partial z}}\\[5pt]
{{\partial f}\over{\partial x}}&{{\partial f}\over{\partial y}}&{{\partial f}\over{\partial z}}\\[5pt]
\end{vmatrix}\\[10pt]
&= \Big( {{\partial^2 f}\over{\partial y \partial z}} - {{\partial^2 f}\over{\partial y \partial z}} \Big) \hat x + \Big( {{\partial^2 f}\over{\partial z \partial x}} - {{\partial^2 f}\over{\partial z \partial x}} \Big) \hat y\\[10pt]
&~~~~~~~~~+\Big( {{\partial^2 f}\over{\partial y \partial x}} - {{\partial^2 f}\over{\partial y \partial x}} \Big) \hat z\\[10pt]
&=0
\end{aligned}윗 식의 첫번째 줄을 행렬식의 형태로 표현하면 두번째 줄이 되며, 벡터곱의 연산규칙을 적용하면 세번째 줄로 전개됩니다. 총 3개의 항으로 분해가 되는데요. 각 괄호안에 있는 수식들이 모두 0이되는 것을 알 수 있어요.
따라서 어떤 스칼라 함수에 대한 기울기의 회전은 항상 0이 됩니다.
\tag{2-2}
\nabla \times (\nabla f) = 03. 회전의 발산(Divergence of a curl)
어떤 벡터함수 \vec v에 대한 회전의 발산(Divergence of a curl)도 항상 0이 됩니다.
이를 기호로 표현하면 \nabla \cdot (\nabla \times \vec v)가 되는데요. 이를 전개해 볼게요. 이것도 정말 0이 되는지 알아봐요.
\tag{3-1}
\begin{aligned}
\nabla \cdot (\nabla \times \vec v) &= \nabla \cdot
\begin{vmatrix}
\hat x & \hat y & \hat z\\
{{\partial}\over{\partial x}} &{{\partial}\over{\partial y}}
&{{\partial}\over{\partial z}}\\
v_x & v_y & v_z
\end{vmatrix}\\[10pt]
&=\nabla \cdot \Big[\Big( {{\partial v_z}\over{\partial y}} - {{\partial v_y}\over{\partial z}}\Big) \hat x + \Big( {{\partial v_x}\over{\partial z}} - {{\partial v_z}\over{\partial x}}\Big) \hat y +\Big( {{\partial v_y}\over{\partial x}} - {{\partial v_x}\over{\partial y}}\Big) \hat z \Big] \\[10pt]
&=\Big({{\partial}\over{\partial x}} \hat x + {{\partial}\over{\partial y}} \hat y + {{\partial}\over{\partial z}}\hat z \Big) \\[10pt]
&~~~~~~~~~~\cdot \Big[\Big( {{\partial v_z}\over{\partial y}} - {{\partial v_y}\over{\partial z}}\Big) \hat x + \Big( {{\partial v_x}\over{\partial z}} - {{\partial v_z}\over{\partial x}}\Big) \hat y +\Big( {{\partial v_y}\over{\partial x}} - {{\partial v_x}\over{\partial y}}\Big) \hat x \Big] \\[10pt]
&={{\partial}\over{\partial x}}\Big( {{\partial v_z}\over{\partial y}} - {{\partial v_y}\over{\partial z}}\Big) + {{\partial}\over{\partial y}} \Big( {{\partial v_x}\over{\partial z}} - {{\partial v_z}\over{\partial x}} \Big) + {{\partial}\over{\partial z}} \Big( {{\partial v_y}\over{\partial x}} - {{\partial v_x}\over{\partial y}}\Big)\\[10pt]
&=0
\end{aligned}위 식의 세번째 줄에 스칼라곱이 들어가 있으므로 전개과정에서 평행한 단위벡터 사이의 스칼라곱은 1이고, 수직한 단위벡터 사이의 스칼라곱은 0이 됩니다.
결국 네번째 줄을 전개해보면 0이 됨을 알 수 있어요. 그래서 어떤 벡터함수에 대한 회전의 발산은 언제든지 0이 됩니다.
\tag{3-2}
\nabla \cdot (\nabla \times \vec v) = 04. 회전의 회전(Curl of a curl)
어떤 벡터 함수 \vec v에 대한 회전의 회전을 구해볼께요. 이때 \nabla \times \vec v는 (3-1)식의 두번째 줄에 전개해 놓은 것이 있으니 그것을 가져올게요.
\tag{4-1}
\begin{aligned}
\nabla \times (\nabla \times \vec v )&=
\begin{vmatrix}
\hat x & \hat y & \hat z\\[10pt]
{{\partial}\over{\partial x}} & {{\partial}\over{\partial y}} & {{\partial}\over{\partial z}}\\[10pt]
{{\partial v_z}\over{\partial y}} - {{\partial v_y}\over{\partial z}} & {{\partial v_x}\over{\partial z}} - {{\partial v_z}\over{\partial x}} & {{\partial v_y}\over{\partial x}} - {{\partial v_x}\over{\partial y}}
\end{vmatrix}\\[10pt]
&={{\partial^2 v_y}\over{\partial x \partial y}} \hat x + {{\partial^2 v_z}\over{\partial x \partial z}} \hat x + {{\partial^2 v_z}\over{\partial y \partial z}}\hat y + {{\partial^2 v_x}\over{\partial x \partial y}}\hat y + {{\partial^2 v_x}\over{\partial x \partial z}} \hat z + {{\partial^2 v_y}\over{\partial y \partial z}}\hat z\\[10pt]
&~~~~~~{\color{blue}+{{\partial^2 v_x}\over{\partial x^2}}\hat x + {{\partial^2 v_y }\over{\partial y^2}}\hat y + {{\partial^2 v_z}\over{\partial z^2}}\hat z } {\color{red}- \Big({{\partial^2}\over{\partial x^2}} + {{\partial^2}\over{\partial y^2}} + {{\partial^2}\over{\partial z^2}}\Big)(v_x \hat x + v_y \hat y + v_z \hat z)}\\[10pt]
&=\Big({{\partial}\over{\partial x}} \hat x + {{\partial}\over{\partial y}}\hat y + {{\partial}\over{\partial z}} \hat z \Big) \Big({{\partial v_x}\over{\partial x}} + {{\partial v_y}\over{\partial y}} + {{\partial v_z}\over{\partial z}}\Big) - \nabla^2 \vec v\\[10pt]
&=\nabla (\nabla \cdot \vec v) - \nabla^2 \vec v
\end{aligned}전개 과정이 어렵진 않은데 조금 복잡해요. 위 식에서 빨강색 부분이 - \nabla^2 \vec v가 됩니다. 식을 이렇게 표현하기 위해 파랑색으로 표현된 항들의 추가가 필요합니다.
꼭 연필잡고 한번만 전개해 보세요.
결국 어떤 벡터함수에 대한 회전의 회전은 다음과 같습니다.
\tag{4-2}
\nabla \times(\nabla \times \vec v) = \nabla(\nabla \cdot \vec v) - \nabla^2 \vec v