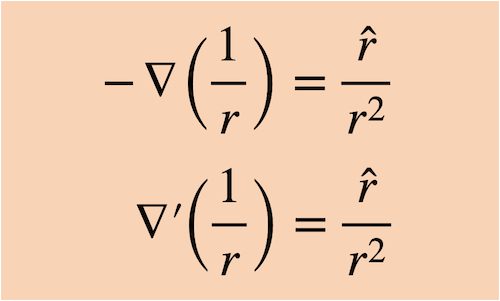1/r 그래디언트 (기울기, gradient)

BallPen · 2025-01-01T10:45:06+09:00

1/r 그래디언트 계산 관계는 전자기학 등에서 자주 활용됩니다. 특히 비프라임좌표계와 프라임좌표계 사이의 그래디언트 변환 관계가 자주 사용됩니다. 이번 글에서는 두 좌표계에서의 (1/r) 그래디언트를 유도해 보겠습니다.

Last Updated on 2025-01-01 by BallPen

직각좌표계에서 1/r 그래디언트를 구해 봐요.

1/r 그래디언트(gradient, 기울기) 결과는 전자기학 등에서 자주 활용되는데요. 이번 글에서는 직각좌표계에서 1/r 그래디언트를 유도해 보겠습니다.

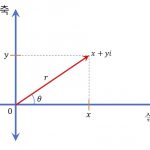
우선 위치벡터 $\vec r$ 이 다음과 같이 주어진다고 생각해봐요.

\tag{D1} \vec r = (x-x^{\prime})\hat i + (y-y^{\prime}) \hat j

그러면 위치 벡터 $\vec r$ 의 크기를 $r$ , 단위벡터를 $\hat r$ 라고 할 때 다음 관계가 성립합니다.

\tag{D2} -\nabla \Big( {1 \over {r}} \Big) = {{\hat r}\over{r^2}}

\tag{D3} \nabla^{\prime} \Big( {1 \over {r}} \Big) = {{\hat r}\over{r^2}}

위 (D2)식에서 $\nabla$ 는 비프라임좌표계인 $xy$ 에 대한 그래디언트 연산을 뜻하고, (D3)식의 $\nabla^{\prime}$ 은 프라임좌표계인 $x^{\prime}y^{\prime}$ 에 대한 그래디언트 연산을 뜻해요.

그럼 이제부터 위 (D2)식과 (D3)식이 실제 성립하는지 알아보겠습니다.

Contents [hide]

(D2)식의 좌변을 풀면 우변이 나오는지 알아 봐요. 우선 (D1)식에 주어진 위치 벡터 $\vec r$ 의 크기는 다음과 같습니다.

\tag{1} r = \sqrt{(x-x^{\prime})^2+ (y - y^{\prime})^2}

이제 위 (1)식을 (D2)식에 대입하고 직각좌표계에서의 그래디언트 연산자를 취하면 다음과 같습니다.

\tag{2} \begin{align} -\nabla \Big({1 \over r} \Big) &= -\Big({{\partial}\over{\partial x}}\hat i + {{\partial}\over{\partial y}}\hat j \Big) {1 \over{\sqrt{(x-x^{\prime})^2+(y-y^{\prime})^2}}}\\[10pt] &=-\Big({{\partial}\over{\partial x}}\hat i + {{\partial}\over{\partial y}}\hat j \Big)\Big[(x-x^{\prime})^2+(y-y^{\prime})^2 \Big]^{-{1 \over 2}}\\[10pt] &=-\Big[ \Big(-{1 \over {\cancel2}}\Big)\Big((x-x^{\prime})^2 + (y-y^{\prime})^2 \Big) ^{-{3 \over 2}} {\cancel 2}(x-x^{\prime}) \Big]\hat i\\[10pt] &~~~~~~~~~~~+\Big[ \Big(-{1 \over {\cancel 2}}\Big)\Big((x-x^{\prime})^2 + (y-y^{\prime})^2 \Big)^{-{3 \over 2}} {\cancel 2}(y-y^{\prime}) \Big]\hat j\\[10pt] &={{(x-x^{\prime})\hat i + (y-y^{\prime})\hat j}\over{[\sqrt{(x-x^{\prime})^2+(y-y^{\prime})^2}}]^2 [\sqrt{(x-x^{\prime})^2+(y-y^{\prime})^2}]}\\[15pt] &={1 \over r^2} {{\vec r}\over{r}}\\[10pt] &={{\hat r}\over{r^2}} \end{align}

위 식의 마지막 두번째 줄에서 마지막 줄로 넘어갈 때 벡터를 벡터의 크기로 나누면 단위벡터가 되는 성질을 이용하였습니다.

정말로 (D2)식이 성립함을 알 수 있어요.

이번에는 (1)식을 (D3)식에 대입하고 직각좌표계에서 프라임좌표에 대한 그래디언트 연산자를 취하면 다음과 같습니다.

\tag{3} \begin{align} \nabla^{\prime} \Big({1 \over r} \Big) &= \Big({{\partial}\over{\partial x^{\prime}}}\hat i + {{\partial}\over{\partial y^{\prime}}}\hat j \Big) {1 \over{\sqrt{(x-x^{\prime})^2+(y-y^{\prime})^2}}}\\[10pt] &=\Big({{\partial}\over{\partial x^{\prime}}}\hat i + {{\partial}\over{\partial y^{\prime}}}\hat j \Big)\Big[(x-x^{\prime})^2+(y-y^{\prime})^2 \Big]^{-{1 \over 2}}\\[10pt] &=\Big[ \Big(-{1 \over {\cancel2}}\Big)\Big((x-x^{\prime})^2 + (y-y^{\prime})^2 \Big) ^{-{3 \over 2}} {\cancel 2}(x-x^{\prime}) (-1) \Big]\hat i\\[10pt] &~~~~~~~~~~~+\Big[ \Big(-{1 \over {\cancel 2}}\Big)\Big((x-x^{\prime})^2 + (y-y^{\prime})^2 \Big)^{-{3 \over 2}} {\cancel 2}(y-y^{\prime}) (-1)\Big]\hat j\\[10pt] &={{(x-x^{\prime})\hat i + (y-y^{\prime})\hat j}\over{[\sqrt{(x-x^{\prime})^2+(y-y^{\prime})^2}}]^2 [\sqrt{(x-x^{\prime})^2+(y-y^{\prime})^2}]}\\[15pt] &={1 \over r^2} {{\vec r}\over{r}}\\[10pt] &={{\hat r}\over{r^2}} \end{align}

정말로 (D3)식이 성립함을 알 수 있어요.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]