Last Updated on 2024-03-04 by BallPen
관성질량 및 중력질량. 이 두 가지 질량이 같은 크기를 가질까요? 아니면 다른 크기를 가질까요?
관성질량 및 중력질량을 쉽게 이해하기 위해서는 관성과 가속도에 대한 아래의 이전 글을 읽고 오시면 좋습니다.
관성질량과 중력질량이란 무엇이고 그 두 질량은 서로 같은 크기를 가질까요? 함께 알아봐요.
아래는 이번 글의 목차입니다.
관성질량 및 중력질량이라는 단어가 낯설수도 있어요. 우리가 물리학을 공부할 때 보통은 질량이라고 하는 하나의 개념만을 배우니까요.
관성질량과 중력질량을 이해하기 위해서는 우선 질량과 관성부터 시작해야 합니다.
1. 질량과 관성
질량은 물질 고유의 양입니다. 그러므로 물체가 우주 어느 곳에 있던 질량은 달라지는 값이 아닙니다. 여기서 힘의 단위를 갖는 무게와 헷갈리시면 안됩니다.
뉴턴 운동의 제1법칙에 따르면 “관성이란 외부에서 힘이 작용하지 않으면 물체는 정지상태 또는 등속직선 운동을 유지하려는 성질”을 말합니다.
이 말을 조금 바꾸면 물체에 힘이 작용하면 물체는 정지상태 또는 등속직선운동을 더이상 유지하지 못한다는 말과 같습니다. 즉, 힘이 작용하면 관성의 법칙이 유지되지 못하고 물체가 가속운동을 하게 된다는 의미이죠.
결국 동일한 힘이 작용할 때 가속도가 작은 물체는 관성이 크고, 가속도가 큰 물체는 관성이 작다고 말할 수 있습니다. 그럼 이러한 관성의 크기는 어느 물리량이 결정할까요? 바로 물체의 질량입니다.
질량이 클수록 관성이 큽니다.
2. 관성질량
위에서 질량이 클수록 관성이 크다고 말했습니다. 이에 대해 조금만 더 알아보겠습니다.
질량이 클수록 관성이 크다면 이 성질을 이용해 어느 물체의 질량값을 구할 수 있을까요?
이를 구하기 위해서는 작용한 힘의 크기 F와 물체의 가속도 a를 알고 있다는 전제하에서 아래의 뉴턴 운동의 제2법칙을 통해 구할 수 있습니다.
\tag{1}
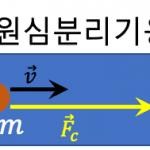
F=ma아래의 [그림 1]을 보세요. t_i = 0인 순간에 질량 m인 물체가 v_i = 0으로 정지상태에 있습니다. 그런데 이 물체에 힘 F가 계속 작용하면 (1)식에 따라 물체는 가속됩니다. 즉 정지상태로부터 점점 빨라지게 되는 것이죠.
![관성질량 [그림 1] 관성질량 구하기. 질량 <span class="katex-eq" data-katex-display="false">m</span>인 물체에 힘 <span class="katex-eq" data-katex-display="false">F</span>가 작용하면 물체는 가속도 <span class="katex-eq" data-katex-display="false">a</span>를 갖고 점점 빨라집니다. 만일 <span class="katex-eq" data-katex-display="false">F</span>와 <span class="katex-eq" data-katex-display="false">a</span>를 우리가 직접 조절하고 측정할 수 있다면 관성질량 <span class="katex-eq" data-katex-display="false">m</span>을 계산할 수 있습니다.](https://ballpen.blog/wp-content/uploads/2021/08/Picture1-3.jpg)
이때 가속도 a는 아래의 식으로 구할 수 있습니다.
\tag{2}
a = {{v_f - v_i}\over{t_f - t_i}}
(2)식에서 v_f와 t_f는 각각 나중속력와 나중시간을 뜻합니다. 그렇다면 실험을 하는 우리가 힘 F를 일정하게 조절할 수 있고, 가속도 a를 측정할 수 있다면 (1)식으로 질량 m을 계산할 수 있을 것입니다.
이렇게 구한 질량 m을 우리는 관성의 성질을 이용해 구한 질량 값이라는 의미에서 관성질량이라고 부릅니다.
만일 관성질량 m인 물체에 힘 F를 가해 가속도 a가 중력가속도 g의 크기와 같은 9.8~\mathrm{m/s^2}이 나오도록 한다면 (1)식에 표기된 가속도 a를 g로 바꾸어 쓸 수 있을 것입니다.
그러면 관성질량을 바로 아래 (3)식과 같이 표현할 수 있어요.
\tag{3} m={F \over g}3. 중력질량
중력질량의 개념은 물체 사이에 작용하는 만유인력, 즉 중력에 관한 식으로부터 출발합니다.
아래 [그림 2]와 같이 M과 m^\prime으로 주어지는 어떤 물리량을 생각해 보세요.
여기서 중요한 것은 이것을 관성질량이라고 단정지어서는 안됩니다. 왜냐면 관성질량은 (3)식과 같이 물체에 힘 F을 가했을 때 물체가 갖는 관성으로부터 구하는 것이기 때문입니다.
그러므로 질량을 갖는 물체사이에 작용하는 중력과는 무관한 현상인것이죠.
그럼 M과 m^\prime을 뭐라고 부를까요? 중력과 관련된 물리량이니 일단 중력질량이라고 불러보겠습니다.
다시한번 말씀드리면 관성질량과 중력질량이 같을 이유가 하나도 없다는 것을 명심하시기 바랍니다.
학교에서 배운 것은 잠시 내려놓으셔도 됩니다.
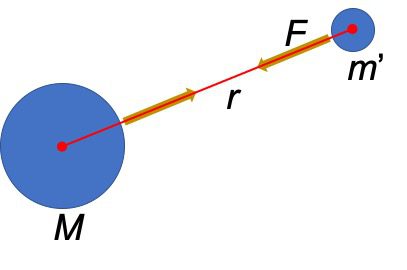
그럼 중력질량을 이용해 실험적으로 정의한 만유인력의 법칙을 쓰면 아래와 같습니다.
\tag{4}
\begin{align}
F &=G {{{m^\prime} M}\over{r^2}} \\
&=m^\prime \Big( {{GM}\over{r^2}} \Big) \\
&=m^\prime g
\end{align}여기서 G는 만유인력상수고, r은 두 물체사이의 떨어진 거리입니다. 그리고 g는 우리가 관심을 두는 중력질량 m^\prime 이외의 모든 요소들로부터 구한 값입니다. 우리는 이것을 보통 중력가속도라고 부릅니다.
결국 (4)식의 가장 마지막 줄로부터 중력질량 m^\prime을 구하면 아래와 같겠군요.
\tag{5}
m^{\prime} = {{F}\over{g}}4. 관성질량 vs 중력질량
(3)식에 주어진 관성질량과 (5)식에 주어진 중력질량이 당연히 같다고 생각하시면 안됩니다. 일단은 다를수도 있다고 생각을 열어두세요.
관성질량과 중력질량이 같은지의 여부는 어떻게 알 수 있을까요? 바로 그 유명한 1971년 달착륙선 아폴로 15호가 수행한 달 표면에서의 실험으로부터 알 수 있었습니다.
아폴로15호의 선장 David Scott이 달 표면에서 해머(hammer)와 깃털을 동시에 자유낙하시키는 실험을 진행했죠. 그 결과 지구에서와는 달리 질량이 큰 해머와 질량이 작은 깃털이 동시에 바닥에 떨어진다는 것을 알게 되었습니다.
이 실험은 공기저항력이 없는 상태에서 자유낙하운동을 시킨 대표적 사례입니다.
자세한 것은 아래 YouTube 영상을 한번 보시죠. 화질은 별로 좋지 않습니다.
Hammer vs Feather – Physics on the Moon – AIRBOYD
이와 같은 실험을 지구안에서도 한 적이 있습니다. 밀폐된 방의 공기를 빼내어 진공상태를 만들고 그 안에서 질량이 서로 다른 두 물체를 자유낙하시키는 것이죠.
아래의 YouTube 영상을 보시죠. 이 영상의 화질은 아주 좋습니다.
Brian Cox visits the world’s biggest vacuum | Human Universe – BBC
영상에서와 같이 공기가 있는 상태에서는 볼링공이 먼저 떨어지지만 진공속에서는 볼링공과 깃털이 동시에 바닥에 떨어지는 것을 명확히 볼 수 있습니다.
이 실험 결과가 뜻하는 의미는 무엇일까요?
바로 중력질량이 큰 물체의 중력가속도나 중력질량이 작은 물체의 중력가속도나 동일하다는 의미입니다. 바꾸어말하면 중력가속도는 중력질량과 무관하게 일정하다는 아주 중요한 의미를 갖습니다.
이를 식으로 표현해보겠습니다.
(5)식을 중력가속도 g에 대해 정리합니다. 그리고 중력질량에 작용하는 중력 F에 (3)식의 관성질량에 작용하는 힘 F를 대입합니다. 즉 물체에 작용하는 중력을 관성질량에 작용하는 힘으로 치환해보는 것이죠.
\tag{6}
g= {{F}\over{m^{\prime}}} = {{m}\over{m^{\prime}}} g(6)식에서 가장 좌변과 우변의 결과값은 서로 동일해야 할 것입니다. 이를 위해서는 m/m^{\prime}의 크기는 무엇이 되어야 할까요?
네 맞습니다. 바로 1이 되어야 합니다. 즉 관성질량 m과 중력질량 m^{\prime}의 크기는 같아야 하는 것입니다.
그래야 중력가속도가 중력질량에 따라 달라지지 않고 상수가 될 수 있는 것입니다. 또한 이를 통해 진공속에서 볼링공과 깃털이 동시에 바닥에 떨어지는 이유를 설명할 수 있습니다.
만일 관성질량과 중력질량이 서로 다르다면 어떻게 될까요? m/m^{\prime}이 1이 아니면 중력가속도는 중력질량에 의존하게 됩니다. 무슨 말이냐면 두 물체가 동시에 바닥에 떨어지는 것이 아니고 볼링공이 먼저 떨어지게 될 것입니다.
5. 정리
- 질량은 한 종류라고 배우는데 엄밀하게는 관성질량과 중력질량이 존재한다. 그리고 원리적으로는 이 둘이 같아야 할 이유는 없다.
- 실험적으로 진공속에서 질량이 서로 다른 물체를 떨어뜨렸을 때 두 물체가 동시에 바닥에 떨어진다. 이것은 중력가속도는 물체의 질량에 따라 달라지지 않음을 의미한다.
- 이러한 성질은 관성질량과 중력질량이 절묘하게 같아야만 벌어지는 현상이다. 그러므로 관성질량과 중력질량의 크기는 서로 같다는 것을 알 수 있다. 이 때문에 보통 관성질량과 중력질량을 구분하지 않고 그냥 질량이라고 표현한다.
- 그런데 관성질량과 중력질량이 절묘하게 같은 이유는 아직 모르지만 같다는 것은 안다. 이것이 아인슈타인 일반상대성이론의 등가원리(equivalence principles)이다.
- 만일 관성질량과 중력질량이 다르다면 진공속에서 서로 다른 질량을 갖는 물체를 떨어뜨릴 때 동시에 바닥에 떨어지지 않을 것이다. 즉 중력가속도가 질량에 의존하게 된다.







1 thought on “관성질량 vs 중력질량 – 진공에서 자유낙하하는 볼링공과 깃털의 운동”