보존력 (Conservative force)

Last Updated on 2023-06-02 by BallPen

보존력의 특성은 무엇이고, 보존력과 비보존력을 구분하는 방법을 알아보겠습니다.

보존력(conservative force)이란 닫힌 경로를 따라 한 일(work)이 0이 되도록 하는 힘을 말합니다. 바꾸어 말하면 어떤 힘이 한 일이 경로에 무관하고 시작점과 끝점에만 의존하는 경우 그 힘을 보존력이라고 해요.

어떤 힘 \vec F가 보존력이라면 다음의 세가지 요건을 만족합니다.

\tag{A-1}
\color{blue}\bold{\oint \vec F \cdot d\vec r = 0}

\tag{A-2}
\color{blue}\bold{\nabla \times \vec F = 0}

\tag{A-3}
\color{blue}\bold{\vec F = - \nabla V}

그럼 이제부터 보존력의 특성이 무엇이고 위에 주어진 세개의 식은 무슨 의미를 갖는지 설명드리겠습니다.

상세하게 설명드리니 차분하게 읽어보시면 도움이 될거에요.

아래는 이번 글의 목차입니다.

1. 보존력 vs. 비보존력

힘은 보존력과 비보존력(nonconservative force)으로 구분할 수 있습니다.

1-1. 보존력 특성

앞에서 설명드렸듯이 닫힌 경로를 따라 보존력이 한 일은 0이고, 비보존력이 한 일은 0이 아닙니다.

이 말을 조금 더 쉽게 말씀드리겠습니다. 이런 경우를 생각해 보세요.

지표면으로부터 10.0 m 위에 어떤 물체를 손으로 잡고 있다가 그 물체를 자유낙하시켰습니다. 그러면 물체는 지구가 당기는 중력 F에 의해 등가속도 운동을 하며 떨어지죠.

이때 공기 저항력은 무시합니다.

등가속도 운동방정식을 적용하면 물체가 지면과 충돌하기 직전의 속도 v를 구할 수 있어요.

\tag{1-1}
\begin{align}
v &= \sqrt{v_0^2 + 2g\Delta y}\\
&=\sqrt{0~\mathrm{m/s} + (2 \times 9.8~\mathrm{m/s^2} \times 10.0~\mathrm{m)}}\\
&=\sqrt{196~\mathrm{m^2/s^2}}\\
&=14.0 ~\mathrm{m/s}
\end{align}

이때 물체는 처음에 정지해 있으므로 초기속도 v_0는 0으로 계산되었어요.

(1-1)식과 같이 중력 F만이 작용하는 상태에서 물체는 지면과 충돌하기 직전에 14.0 m/s의 속도를 갖습니다.

그렇다면 지면에서 수직 위쪽방향으로 14.0 m/s의 빠르기로 동일한 물체를 던져 올린다면 그 물체는 10.0 m까지 올라갈 수 있을까요?

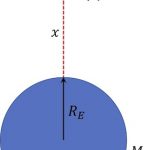
아래 [그림 1]은 그 상황을 나타낸 그림입니다.

물체는 낙하할 때와 던져 올려질 때 모두 지구 중심을 향하는 중력 F를 받습니다. 이 상황에서 14.0 m/s의 빠르기로 위쪽으로 던져진 물체는 10.0 m까지 올라갈 수 있어요.

이와 같이 중력이 작용하는 공간에서 물체를 자유 낙하시킨 후, 지면과 충돌하기 직전의 빠르기로 반대방향으로 던지면 그 물체는 최초의 높이까지 똑같이 올라가게 됩니다.

이와 같이 중력 F는 물체가 낙하할 때나 위로 던져졌을 때 동일한 물리 현상을 일으킵니다. 이러한 힘을 보존력이라고 부릅니다.

1-2. 비보존력 특성

위에서 설명드렸듯이 중력은 보존력이에요. 그렇다면 중력이 작용하는 동안 공기저항력이 동시에 작용한다면 어떻게 될까요?

물론 공기저항력도 힘의 한 종류입니다. 다만 이 힘은 물체의 운동 속도와 반대방향으로 작용해요.

따라서 물체가 높은 곳에서 떨어질 때 중력 F는 지구 중심방향을 향하지만 공기저항력 F^{\prime}은 반대 방향인 위쪽 방향을 향합니다.

따라서 두 힘은 서로 상쇄되어 물체에 작용하는 알짜힘을 감소시킵니다. 결국 물체가 낙하하는 동안의 가속도도 감소되죠.

이 상황을 표현한 것이 [그림 2]입니다.

그림과 같이 10.0 m에서 낙하한 물체는 공기저항력이 없을 때의 빠르기인 14.0 m/s보다 줄어든 12.0 m/s로 지면과 충돌합니다. 이때 12.0 m/s는 임의로 결정한 수치임을 주의하세요. 계산된 값이 아닙니다.

그렇다면 12.0 m/s의 빠르기로 수직 위쪽으로 던져올린다면 10.0 m까지 올라갈 수 있을까요? 아닙니다.

낙하할 때 뿐만 아니라 위쪽으로 올라갈 때에도 보존력인 중력 F가 여전히 작용하지만 물체의 움직임과 반대방향으로 공기저항력 F^{\prime}도 작용하여 물체는 10.0 m까지 절대로 올라가지 못합니다.

이와 같이 보존력인 중력만 작용하는 경우와는 달리, 공기저항력이 추가적으로 개입하는 경우에는 물체가 떨어질 때나 올라갈 때 물리 현상이 달라집니다.

이 말은 물체가 낙하할 때나 던져 올려졌을 때 지표면으로부터 고정된 높이점을 지나가는 물체의 빠르기가 서로 다르다는 의미입니다.

이러한 물리 현상의 차이를 일으키는 공기저항력을 우리는 비보존력이라고 합니다.

2. 보존력 요건

그렇다면 어떤 힘이 보존력인지 비보존력인지 구분할 수 있는 정량적인 방법이 있으면 좋을 것 같아요.

이때 사용하는 요건이 총 3개가 있는데요. 바로 (A-1)에서 (A-3)식으로 주어진 식들입니다.

우선 (A-3)식부터 말씀드릴게요. 그리고 (A-1), (A-2)식 순서로 진행하겠습니다.

2-1. 보존력일때 위치에너지 정의 가능

물체에 작용하는 힘이 보존력이면 물체의 위치에 따른 위치에너지를 정의할 수 있습니다. 바꾸어 말하면 위치에너지가 이미 정해져 있다면 그때 관여하는 힘은 보존력임을 뜻해요.

위치에너지는 역학적에너지 보존 법칙을 만들어 가는 과정에서 정의됩니다. 이를 통해 임의 위치에서의 운동에너지와 위치에너지의 합이 항상 일정하게 됩니다.

따라서 중력이 물체에 작용한다면 바닥으로부터의 높이에 따른 위치에너지를 정의할 수 있어요. 그 이유는 [그림 1]에서와 같이 물체는 떨어질 때나 던져 올려질 때 물리현상이 동일하여 임의 지점에서의 위치에너지와 운동에너지의 합이 항상 일정하도록 아래 (2-1)식의 역학적 에너지 보존 식을 만들 수 있기 때문이에요.

\tag{2-1}
{1 \over 2} mv_0^2 + V(x_0) = {1 \over 2} mv^2 + V(x)

그러나 비보존력이 작용하면 위치에너지를 정의할 수 없어요.

왜냐면 비보존력의 크기에 따라 물체가 내려올 때와 던져올려질 때 바닥으로부터 동일한 높이일지라도 물체의 운동속도가 서로 달라 운동에너지가 다르고, 결과적으로 위치에너지도 달라져야 하기 때문이에요.

위치에너지는 말 그대로 위치가 고정되면 하나의 값으로 정의되어야 하는데 그때 그때 다르면 위치에너지를 정의할 의미가 없는 것이죠.

보존력이 작용할 때 일차원에서 위치에너지 V(x)를 정의하는 식은 아래와 같아요.

\tag{2-2}
\begin{align}
&F(x)dx = - dV(x)\\[11pt]
&F(x) = - {dV(x) \over dx}
\end{align}

(2-2)식을 3차원으로 확장하여 힘을 \vec F로 일반화하고, \vec F에 관한 식을 편미분으로 표현하면 다음과 같습니다.

\tag{2-3}
\begin{align}
\vec F &= - \Big( {\partial V \over \partial x}\hat x + {\partial V \over \partial y}\hat y+{\partial V \over \partial z}\hat z\Big)\\[11pt]
&=- \Big({\partial \over \partial x }\hat x+ {\partial \over {\partial y}}\hat y + {\partial \over \partial z}\hat z \Big)V\\[11pt]
&=- \nabla V
\end{align}

이때 \nabla는 그래디언트(gradient)라고 부르며, 3차원 모든 방향의 기울기를 구하는 벡터 연산자입니다.

정리하면 (2-3)식과 같이 위치에너지의 기울기에 -1을 곱하면 보존력 벡터를 구할 수 있습니다.

중요한 것은 \vec F가 보존력인 경우에만 위치에너지 V를 정의할 수 있다는 거에요. 결국 어떤 문제에서 위치에너지가 이미 주어져 있다면 그때 작용하는 힘은 보존력임을 뜻해요.

2-2. 닫힌 경로에서 보존력이 한 일은 0

(A-1)식 처럼 닫힌 경로에 대해 보존력이 한 일을 구하면 0이 됩니다. 바꾸어 말하면 닫힌 경로에 대해 비보존력이 한 일은 0이 되지 않는다는 의미도 성립합니다.

정말 보존력이 작용할 때 닫힌 경로에 대해 일을 하면 0이 될까요?

아래 [그림 3]은 [그림 1]을 조금 수정한 거에요.

물체에 번호가 써 있는데요.

물체가 \textcircled{1}번에서 중력 \vec{F}_y를 받으며 변위 \Delta \vec{y} = 10.0~\mathrm{m}만큼 낙하합니다. 이때 아래첨자 y는 힘의 방향이 수직방향성분만을 갖는다는 것을 의미해요.

그리고 \textcircled{2}번에서 \textcircled{3}번 방향으로 중력 \vec{F}_y와 수직한 방향으로 변위 \Delta \vec{x} = 6.0~\mathrm{m}만큼 물체를 이동시킵니다.

이와 같은 방식으로 \textcircled{3}번에서 \textcircled{4}번으로 물체를 이동시키고, \textcircled{4}번에서 \textcircled{1}번 방향으로 이동시킵니다.

결국 물체는 중력 \vec{F}_y가 일정하게 작용하는 상태에서 위치 (x,y)\rightarrow(x,y+\Delta y)\rightarrow(x+\Delta x, y+\Delta y) \rightarrow (x+\Delta x , y)\rightarrow(x,y)의 경로를 따라 한바퀴 돌아 최초의 위치로 돌아옵니다.

이 과정에서 중력이 한 일 W를 구해 보겠습니다.

\tag{2-4}
\begin{align}
W &= \oint\vec{F}_y \cdot d\vec r\\[11pt]
&=\int_{y}^{y+\Delta y} \vec{F}_y \cdot d\vec{y} +\color{red} \int_x^{x+\Delta x} \vec {F}_y \cdot d \vec{x}\\[11pt]
&~~~~~~~~~~~~~~~+\color{black}\int_{y+\Delta y}^{y} \vec{F}_y \cdot d\vec{y} \color{red}+ \int_{x+\Delta x}^{x} \vec{F}_y \cdot d\vec x\\[11pt]
&=\int_{y}^{y+\Delta y} \vec{F}_y \cdot d\vec{y}+\color{black}\int_{y+\Delta y}^{y} \vec{F}_y \cdot d\vec{y}\\[11pt]
&=\int_{y}^{y+\Delta y} \vec{F}_y \cdot d\vec{y}-\color{black}\int_{y}^{y+\Delta y} \vec{F}_y \cdot d\vec{y}\\[11pt]
&=0

\end{align}

위 식에서 빨강색 항은 0이 됩니다. 왜냐면 중력은 y방향이지만 변위가 x방향이어서 서로 수직하기 때문이에요. 따라서 내적의 성질에 따라 힘과 변위 사이의 각도가 90도가 되어 \vec{F}_y \cdot d \vec {x}는 F_y dx \cos 90^{\circ}가 되어 0이 됩니다.

(2-4)식과 같이 보존력인 중력이 작용하는 동안 닫힌 경로에 대해 한 일은 정말로 0이 됨을 알 수 있습니다.

그러면 닫힌 경로가 사각형 모양이 아닌 원형 모양으로 달라지면 0이 아닐수도 있을 거라고 생각할 수 있는데요. 경로를 달리하더라도 똑같이 0이됩니다. 이러한 특성을 “보존력이 한 일은 경로에 의존하지 않는다”라고 말합니다.

관련 예제를 풀어보겠습니다.

[예제]

(예제) 힘 \vec F = 3y \hat x + 3x \hat y로 주어질 때, 이 힘이 보존력인지의 여부를 증명하여라.

이 힘이 닫혀진 경로를 따라 한 일이 0이면 보존력입니다.

경로를 아래 (그림 4)처럼 (x,y)\rightarrow(x+\Delta x,y)\rightarrow(x+\Delta x, y+\Delta y) \rightarrow (x, y+\Delta y)\rightarrow(x,y)설정하겠습니다.

\textcircled{1}번 경로부터 \textcircled{4}번 경로까지 한 일을 구체적으로 구하면 다음과 같아요. 조금 복잡해 보여도 연필을 잡고 직접 풀어보면 쉽게 할 수 있을거에요.

\tag{2-5}
\begin{align}
W &= \oint\vec{F} \cdot d\vec r\\[11pt]
&=\int_{x}^{x+\Delta x}F_x(y)dx +  \int_{y}^{y+\Delta y} F_{y}(x+\Delta x)dy\\[11pt]
&~~~~~~~~~~~~~~~~+\int_{x+\Delta x}^{x} F_x(y+\Delta y) dx + \int_{y+\Delta y}^{y} F_y (x)dy\\[11pt]
&\color{blue}=\int_{x}^{x+\Delta x} \Big[ F_{x}(y)-F_{x}(y+\Delta y)\Big] dx\\[11pt]
&~~~~~~~~~~~~~~~~\color{blue}+\int_{y}^{y+\Delta y} \Big[ F_{y} (x+\Delta x) - F_{y}(x) \Big] dy\\
&=\int_{x}^{x+\Delta x} \Big[ 3y-3(y+\Delta y)\Big] dx\\[11pt]
&~~~~~~~~~~~~~~~~+\int_{y}^{y+\Delta y} \Big[ 3(x+\Delta x) - 3x \Big] dy\\[11pt]

&=-3\Delta y\int_{x}^{x+\Delta x}dx + 3 \Delta x \int_{y}^{y+\Delta y}dy\\[11pt]
&= -3\Delta x \Delta y + 3 \Delta x \Delta y\\[11pt]
&=0
\end{align}

위 식의 두번째 줄에서 적분기호 안에 있는 F_{x}(y)가 뜻하는 것은 힘 F의 x성분인 F_x에 y가 고정된 값을 가지니 상수로 대입하라는 뜻입니다.

왜냐면 \textcircled{1}번 경로에서 y값은 변하지 않기 때문이에요. 따라서 F_{x}가 3y이므로 그대로 3y를 적용하면 됩니다.

이와 동일한 방식으로 F_{y}(x+\Delta x)는 힘 F의 y성분에 고정된 값 (x+\Delta x)를 대입하라는 뜻입니다. 즉 F_{y}가 3x이므로 x대신에 x+\Delta x를 대입하여 3(x+\Delta x)로 계산하면 됩니다.

결국 (2-5)식과 같이 \vec F = 3y \hat x + 3x \hat y가 닫힌 경로에 대해 한 일은 0이므로 이 힘은 보존력입니다.

2-3. 보존력의 회전은 0

(A-2)식은 보존력 장의 회전(curl)은 0임을 뜻합니다. 이 관계는 (2-5)식을 약간만 수정하면 도출할 수 있어요.

아래 식은 위 (2-5)식의 상단 부분입니다.

\tag{2-6}
\begin{align}
W &= \oint\vec{F} \cdot d\vec r\\[11pt]

&\color{blue}=\int_{x}^{x+\Delta x} \Big[ F_{x}(y)-F_{x}(y+\Delta y)\Big] dx\\[11pt]
&~~~~~~~~~~~~~~~~\color{blue}+\int_{y}^{y+\Delta y} \Big[ F_{y} (x+\Delta x) - F_{y}(x) \Big] dy\\
\end{align}

파랑색 수식에서 적분기호 안에 F_{x} (y+\Delta y)가 있는 부분을 볼 수 있어요.

이것은 y에서 아주 가까운 y+\Delta y에서의 F_x를 뜻합니다. 이때 아주 가깝다는 뜻은 \Delta y가 1보다 아주 작다는 것을 뜻해요.

임의함수 f(x)에 대해 테일러급수를 적용하면 파랑색 수식을 바꾸어 쓸 수 있어요. 테일러 급수에서 앞의 두번째 항까지만을 나타내면 다음과 같습니다.

\tag{2-7}
f(x) = f(a) + (x-a) f^{\prime}(a)

이 식에서 x \rightarrow x+\Delta x 로 a \rightarrow x로 바꾼다면 (2-7)식을 다음 식으로 바꿀 수 있어요.

\tag{2-8}
\begin{align}
f(x+ \Delta x) &= f(x) + (x+\Delta x - x) f^{\prime}(x)\\[11pt]
&=f(x) + (\Delta x) f^{\prime}(x)
\end{align}

이때 윗식의 임의함수 f를 F_x 또는 F_y로 본다면 F_x (y+\Delta y), F_y (x+\Delta x)를 다음 (2-9)식과 같이 표현할 수 있습니다.

또한 변수가 2개이므로 편미분이 활용됩니다.

\tag{2-9}
\begin{align}
&F_x (y+ \Delta y) = F_x (y) + (\Delta y) {\partial F_x \over \partial y}|_y\\[11pt]
&F_y (x+\Delta x) = F_y (x) + (\Delta x) {\partial F_y \over \partial x}|_x
\end{align}

이제 (2-9)식을 (2-6)식에 대입하고 정리합니다.

\tag{2-10}
\begin{align}
W &= \oint\vec{F} \cdot d\vec r\\[11pt]

&\color{blue}=\int_{x}^{x+\Delta x} \Big[ F_{x}(y)-F_{x}(y+\Delta y)\Big] dx\\[11pt]
&~~~~~~~~~~~~~~~~\color{blue}+\int_{y}^{y+\Delta y} \Big[ F_{y} (x+\Delta x) - F_{y}(x) \Big] dy\\[11pt]
&=\int_x^{x+\Delta x} \Big[ \cancel {F_x (y)} - \cancel{F_x (y)} - (\Delta y) {{\partial F_x}\over{\partial y}}|_y \Big] dx \\[11pt]
&~~~~~~~~~~~~~~~~+\int_y^{y+\Delta y } \Big[ \cancel{F_y (x)} + (\Delta x) {\partial F_y \over \partial x}|_x - \cancel{F_y (x)} \Big ]dy\\[11pt]
&=-(\Delta y) {{\partial F_x}\over{\partial y}} \int_x^{x+\Delta x} dx + (\Delta x) {{\partial F_y}\over{\partial x}} \int_y^{y+\Delta y}dy\\[11pt]
&={{\partial F_y}\over{\partial x}} \Delta x \Delta y - {{\partial F_x}\over{\partial y}}\Delta x \Delta y\\[11pt]
&=\Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}} \Big) \Delta x \Delta y\\[11pt]
\end{align}

어느정도 정리가 되었는데요. (2-10)식은 힘이 보존력이라면 닫힌 경로에 대해 한 일이 0이어야 하므로 다음의 조건을 만족해야 합니다.

\tag{2-11}
\begin{align}
W &=\oint \vec F \cdot d\vec r \\[11pt]
&= \color{red}\Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}} \Big) \color{black}\Delta x \Delta y\\
&=0
\end{align}

이때 윗식에서 \Delta x와 \Delta y는 초기 조건상 0이 될 수 없으므로 괄호안에 있는 빨강색 부분이 0이 되어야만 합니다.

\tag{2-12}
\begin{align}
 \color{red}\Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}} \Big) 
&=0
\end{align}

[Stokes의 정리]

(2-11)식을 통해 (2-12)식이 도출되었는데요. 이것은 [그림 4]처럼 힘 \vec F가 xy 평면상에 존재하는 경우에 한정됩니다.

보존력 장은 xy평면 뿐만 아니라 yz 평면, zx평면에도 존재할 수 있는거에요. 그래서 (2-11)식을 일반화할 필요가 있습니다.

(2-11)식을 보면 좌변은 일 W로서 스칼라량입니다. 그러나 우변은 벡터량인 힘의 각성분들을 x와 y로 미분하므로 벡터로서 표현되는 것이 맞습니다.

그러므로 (2-11)식에서 빨강색 부분이 벡터로서 표현되어야 한다면 \Delta x \Delta y도 면적벡터로 바꾸고 두 벡터를 내적하면 스칼라가 될 것을 짐작할 수 있습니다. 이때 면적벡터의 방향은 오른손 법칙을 적용하여 xy 평면에 수직한 \hat z방향으로 결정하면 합리적이죠.

이러한 상황을 반영해서 (2-11)식을 엄밀하게 다시 쓰면 다음과 같아요.

\tag{2-13}
\begin{align}
W_{xy} &=\oint \vec F \cdot d\vec r \\[11pt]
&= \color{red}\Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}} \Big) \hat z \cdot \Big( \Delta x \Delta y\Big)\hat z\\[11pt]
&=\color{d}\Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}} \Big) \Big( \Delta x \Delta y\Big)\\[11pt]
&=0
\end{align}

이 관계를 yz 평면, zx평면에 대해서도 적용하면 아래와 같습니다.

\tag{2-14}
\begin{align}
W_{yz} &=\oint \vec F \cdot d\vec r \\[11pt]
&= \color{red}\Big( {{\partial F_z}\over{\partial y}} - {{\partial F_y}\over{\partial z}} \Big) \hat x \cdot \Big( \Delta y \Delta z\Big)\hat x\\[11pt]
&= \color{d}\Big( {{\partial F_z}\over{\partial y}} - {{\partial F_y}\over{\partial z}} \Big)  \Big( \Delta x \Delta y\Big)\\[11pt]
&=0
\end{align}

\tag{2-15}
\begin{align}
W_{zx} &=\oint \vec F \cdot d\vec r \\[11pt]
&= \color{red}\Big( {{\partial F_x}\over{\partial z}} - {{\partial F_z}\over{\partial x}} \Big) \hat y \cdot \Big( \Delta z \Delta x\Big)\hat y\\[11pt]
&= \color{d}\Big( {{\partial F_x}\over{\partial z}} - {{\partial F_z}\over{\partial x}} \Big)  \Big( \Delta z \Delta x\Big)\\
&=0
\end{align}

결국 (2-13), (2-14), (2-15)식을 종합하여 일반화할 경우 보존력 장이 닫힌 경로에 대해 한 일이 0이 되기 위해서는 ‘Stokes 정리‘라고 불리는 다음 (2-16)식이 0이 되어야 합니다.

\tag{2-16}
\oint \vec F \cdot d\vec r = \int_s (\nabla \times \vec F) \cdot d\vec a

이때 우변의 적분기호 안에 있는 \nabla \times \vec F를 ‘curl \vec F‘ 또는 ‘\vec F의 회전’이라고 부릅니다.

‘curl \vec F‘ 는 (2-13), (2-14), (2-15)식에서 빨강색 수식에서의 편미분 항을 종합한 개념입니다.

\tag{2-17}
\begin{align}
\nabla \times \vec F &= \Big( {{\partial F_z}\over{\partial y}} - {{\partial F_y}\over{\partial z}}  \Big) \hat x \\[11pt]
&~~~~~~~~~~~~~+ \Big( {{\partial F_x}\over{\partial z}} - {{\partial F_z}\over{\partial x}}  \Big) \hat y \\[11pt]
&~~~~~~~~~~~~~~~~~~~~~~+ \Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}}  \Big) \hat z 
\end{align}

결국 (2-16)식이 0이되기 위해서는(2-17)식으로 주어진 ‘F의 회전’이 0이되어야만 합니다.

\tag{2-18}
\nabla \times \vec F = 0

[예제]

(예제) 힘 \vec F_1 = 3y \hat x + 3x \hat y와, \vec F_2 = -3y \hat x + 3x \hat y가 각각 보존력인지의 여부를 (2-17)식을 이용하여 증명하여라.

힘 \vec F_1 = 3y \hat x + 3x \hat y을 z성분까지 쓰면 다음과 같습니다.

\tag{2-19}
\vec F_1 = 3y \hat x + 3x \hat y + 0 \hat z

(2-19)식을 (2-17)식에 대입하고 정리합니다.

\tag{2-20}
\begin{align}
\nabla \times \vec F_1 &= \Big( {{\partial F_z}\over{\partial y}} - {{\partial F_y}\over{\partial z}}  \Big) \hat x + \Big( {{\partial F_x}\over{\partial z}} - {{\partial F_z}\over{\partial x}}  \Big) \hat y + \Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}}  \Big) \hat z \\[11pt]
&=\Big( {{\partial 0}\over{\partial y}} - {{\partial 3x}\over{\partial z}}  \Big) \hat x + \Big( {{\partial 3y}\over{\partial z}} - {{\partial 0}\over{\partial x}}  \Big) \hat y + \Big( {{\partial 3x}\over{\partial x}} - {{\partial 3y}\over{\partial y}}  \Big) \hat z \\[11pt]
&=0 \hat x + 0 \hat y + (3-3) \hat z\\[11pt]
&=0
\end{align}

위와 같이 \nabla \times \vec F_1가 0이므로 \vec F_1은 보존력입니다.

동일한 방식으로 \vec F_2 = -3y \hat x + 3x \hat y도 z성분까지 쓰면 다음과 같습니다.

\tag{2-21}
\vec F_2 = -3y \hat x + 3x \hat y + 0 \hat z

(2-21)식을 (2-17)식에 대입하고 정리합니다.

\tag{2-22}
\begin{align}
\nabla \times \vec F_2 &= \Big( {{\partial F_z}\over{\partial y}} - {{\partial F_y}\over{\partial z}}  \Big) \hat x + \Big( {{\partial F_x}\over{\partial z}} - {{\partial F_z}\over{\partial x}}  \Big) \hat y + \Big( {{\partial F_y}\over{\partial x}} - {{\partial F_x}\over{\partial y}}  \Big) \hat z \\[11pt]
&=\Big( {{\partial 0}\over{\partial y}} - {{\partial 3x}\over{\partial z}}  \Big) \hat x + \Big( {{\partial (-3y)}\over{\partial z}} - {{\partial 0}\over{\partial x}}  \Big) \hat y + \Big( {{\partial 3x}\over{\partial x}} - {{\partial (-3y)}\over{\partial y}}  \Big) \hat z \\[11pt]
&=0 \hat x + 0 \hat y + (3+3) \hat z\\[11pt]
&=6 \hat z
\end{align}

위와 같이 \nabla \times \vec F_2가 0이 아니므로 \vec F_2는 비보존력입니다.

[벡터 장의 회전]

힘 \vec F_1 = 3y \hat x + 3x \hat y와 \vec F_2 = -3y \hat x + 3x \hat y는 공간의 각 점을 벡터로 표현할 수 있습니다.

이와 같이 공간상의 각 점을 벡터로 표현한 것을 벡터장(vector field)이라고 합니다.

또한 이러한 벡터장에 회전을 취한 것이 바로 \nabla \times \vec F 이죠.

그런데 벡터장에 회전을 취하는 이유는 무엇일까요? 그 이유는 벡터장의 회전적 성질의 대표값을 구하기 위함입니다. 만약 벡터장의 회전적 성질이 강하다면 \nabla \times \vec F 의 크기가 클 것이고, 회전적 성질이 약하다면 \nabla \times \vec F 의 크기가 작을 것입니다.

이를 명확히 알아보기 위해 위에서 정의한 \vec F_1과 \vec F_2의 벡터장을 그려보면 아래와 같습니다.

먼저 [그림 5]는 \vec F_1 = 3y \hat x + 3x \hat y의 벡터장입니다.

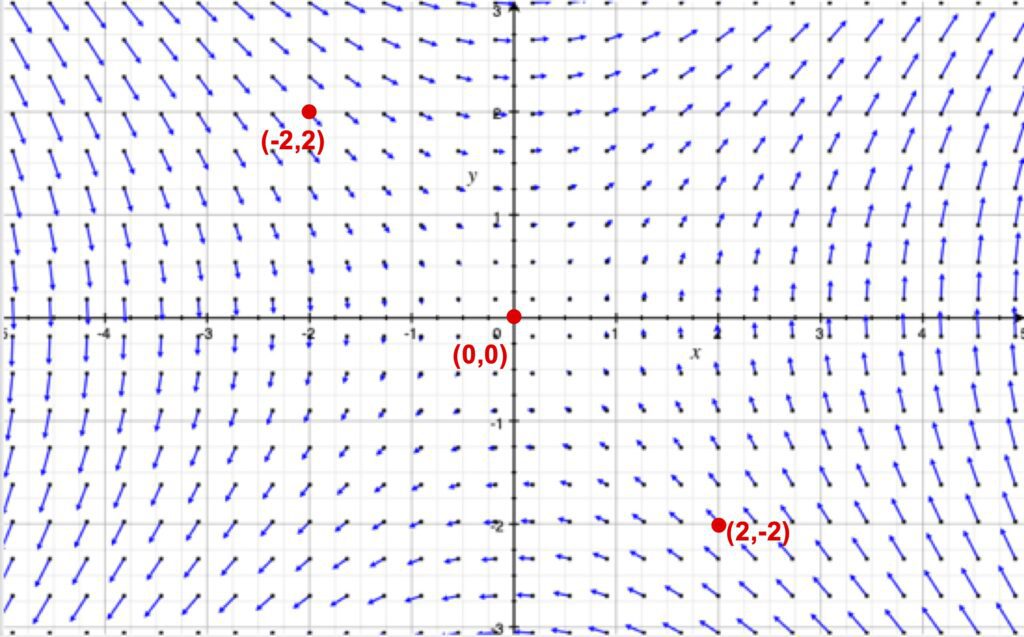
이 보존력의 벡터장은 (2-20)식의 결과에 따라 벡터장의 회전이 0이므로 회전하지 않습니다.

또한 위치 (-2,2)에서 물체를 놓으면 물체는 가속되어 원점 (0,0)을 지나 (2,-2)까지 도달 한 후 방향을 바꾸어 다시 원점을 지나 최초의 위치인 (-2,2)까지 돌아옵니다.

따라서 위치에너지를 정의할 수 있고 어느 좌표에서든 총 역학적 에너지는 모두 동일합니다.

이번에는 \vec F_2 = -3y \hat x + 3x \hat y에 대한 벡터장을 [그림 6]에 나타내었습니다.

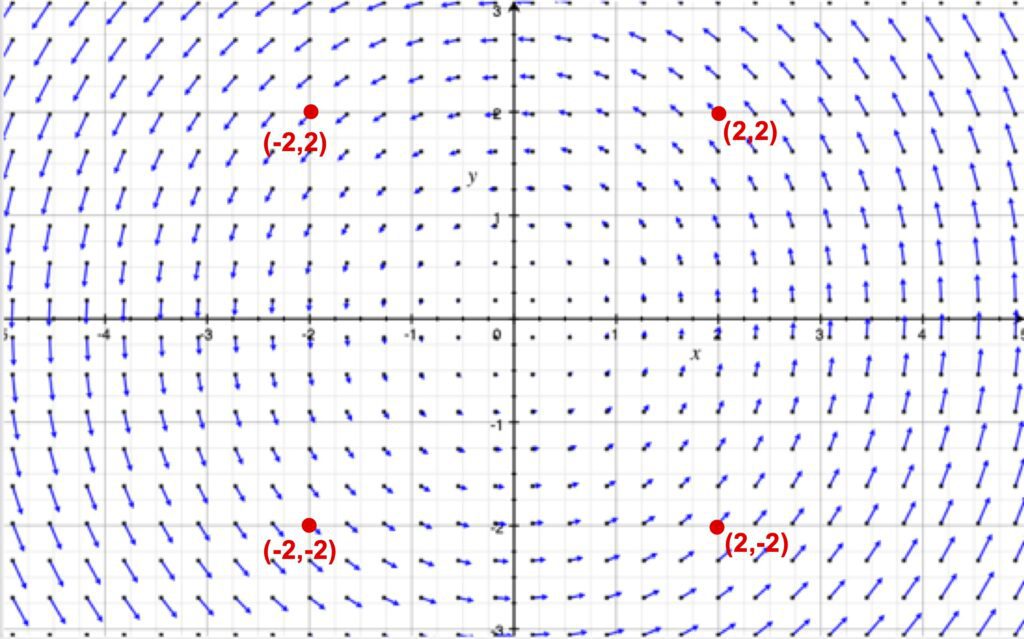
이 비보존력 장의 벡터장은 (2-22)식의 결과에 따라 벡터장의 회전이 0이 아니며 z축을 중심으로 회전합니다.

또한 위치 (-2,2)에서 물체를 놓으면 물체는 힘의 장을 따라 (-2,-2), (2,-2), (2,2)의 경로로 회전하여 (-2,2)로 되돌아 올것을 짐작할 수 있습니다.

그런데 이 회전 경로를 따라 물체가 계속 회전하면 어떻게 될까요? 회전할 때 마다 물체의 속도가 점점 증가할 거에요. 그러므로 한 지점에 대응하는 고유의 위치에너지를 정의하는 것이 불가능합니다.

바꾸어 말하면 총 역학적 에너지는 보존이 되지 않습니다.

마지막으로 보존력의 예시로는 중력, 탄성력, 전기력 등이 있으며, 비보존력에는 마찰력, 공기저항력 등이 있습니다.

Related posts.

역학적 에너지 보존 자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 풍량과 풍량효율 측정 및 계산법이 궁금한가요 단위 – SI 단위, 10의 거듭제곱, 접두어 및 올바른 단위 표기법 SEM 이론 – (1) 주사전자현미경과 관련된 기초 물리학 이론 조명 – 단색광, 다색광, 복사선속, 광선속, 광도, 조도, 휘도의 완벽 정리 유효 숫자 계산 예제 로그 기본 성질과 로그 활용 사례