전기장의 발산(Divergence of Electric field)

Last Updated on 2024-04-14 by BallPen

전기장의 발산을 계산하고 그 결과가 갖는 의미를 알아봐요.

전기장의 발산(divergence)과 물리적 의미를 알아보겠습니다.

전하가 만드는 장(field)을 전기장이라고 하는데요. 전기장은 양전하에서 나와 음전하로 들어가죠. 전기장의 발산 공식(divergence theorem)은 다음과 같이 주어집니다.

\tag{D1}
\oint_s \vec E \cdot d \vec a = \int_V (\color{red}{\nabla \cdot \vec E} \color{black})d\tau = {1 \over \epsilon_0}\int_V \rho (\vec r) d \tau = {{Q_{enc}}\over{\epsilon_0}}

이때 빨강색으로 표기한 \nabla \cdot \vec E를 전기장의 발산이라고 하는데요. 그것만을 따로 쓰면 다음 식이 성립해요.

\tag{D2}
\begin{align}
\nabla \cdot \vec E ={{ \rho (\vec r)} \over{\epsilon_0}}
\end{align}

과연 (D2)식은 어떻게 유도될까요?

우선 가우스 법칙을 복습하고 전기장의 발산을 설명드릴께요. 아래는 이번 글의 목차입니다.

1. 가우스법칙 복습

(D1)식의 발산정리에서 가장 왼쪽에 있는 좌변와 가장 오른쪽의 우변을 연결하면 아래식이 됩니다.

\tag{1-1}
\oint_s \vec E \cdot d \vec a = {{Q_{enc}}\over{\epsilon_0}}

이 식을 가우스 법칙이라고 해요.

가우법 법칙의 좌변은 전기장을 닫힌 곡면에 대해 적분한 것으로 이를 전기장 선속(electric flux)이라고 불러요. 그런데 그 전기장 선속이 닫힌 곡면 내에 있는 알짜 전하량 Q_{enc}을 \epsilon_0로 나눈 값과 같다는 것이죠

물론 닫힌 곡면내에 알짜전하가 없다면 Q_{enc}=0이므로 전기장 선속은 0이 됩니다.

그렇다면 (D1)식에서 중간에 끼워져 있는 두 식은 뭘까요? 이제부터 그 내용을 알아보겠습니다.

2. 전기장의 발산

2-1. 점전하가 만드는 전기장

전하 하나를 보통 점전하라고 하는데요. 점전하의 전하량을 q라고 할 때 \vec r만큼 떨어진 곳에서의 전기장 \vec E는 다음과 같습니다.

\tag{2-1}
\vec E = {1 \over{4 \pi \epsilon_0}}{\hat r q \over{r^2}} 

여기서 \hat r은 단위벡터를 뜻합니다.

2-2. 연속전하가 만드는 전기장

그런데 이러한 점전하들이 모여 연속적인 전하분포를 이룬다고 생각해봐요. [그림 1]은 그러한 상황을 나타낸거에요.

이때 좌표계의 원점을 임의 장소로 잡았어요. 그림과 같이 전하분포 내부일수도 있고 전하분포 밖일 수도 있어요. 중요한 것은 여러분들이 선택한 어느 기준위치가 원점이라는 것을 기억해주세요.

그리고 연속 전하분포가 갖는 공간의 미소 부피요소를 d \tau^{\prime}이라 하고, 이 부피 요소 안에 있는 미소 전하량을 dq라고 해봐요.

그러면 그곳에서의 전하 밀도 \rho(\vec {r^{\prime}})는 단위부피당 전하량으로 dq = \rho d \tau의 관계가 성립합니다.

그러면 미소 전하량 dq에 의한 \vec {r^{\prime \prime}} 인 지점에서의 미소 전기장은 다음과 같이 주어져요.

\tag{2-2}
\begin{align}
d \vec E &= {{1}\over{4 \pi \epsilon_0}} {{\hat r^{\prime\prime}dq}\over{{r^{\prime \prime}}^2}}={{1}\over{4 \pi \epsilon_0}}{{ \hat r ^{\prime\prime}\rho(\vec {r^{\prime}}) d\tau^{\prime}}\over{{r^{\prime \prime}}}^2}
\end{align}

그리고 (2-2)식을 전체 공간에 대해 적분하면 다음과 같아요.

\tag{2-3}
\begin{align}
\vec E &={1 \over{4 \pi \epsilon_0}} \int_{all~space} {{\hat r^{\prime\prime}\rho(\vec {r^{\prime}}) }\over{{r^{\prime \prime}}^2}} d\tau^{\prime}
\end{align}

여기서 적분기호 아래에 있는 all~space는 r^{\prime \prime}=0인 지점을 포함한다는 의미에요. 이것은 곧 델타함수(delta function)를 활용한다는 의미가 됩니다.

이제 전기장을 정의했으니 전기장의 발산을 구해봐요.

2-3. 전기장의 발산 계산

(2-3)식의 좌변과 우변에 발산을 취합니다. 그것이 전기장의 발산이죠. 그러면 다음과 같아요.

\tag{2-4}
\begin{align}
\nabla \cdot \vec E &= \nabla \cdot\Big({1 \over{4 \pi \epsilon_0}} \int_{all~space} {{\hat r^{\prime\prime}\rho(\vec {r^{\prime}}) }\over{{r^{\prime \prime}}^2}} d\tau^{\prime}\Big)\\[10pt]
&={1 \over{4 \pi \epsilon_0}} \int \nabla \cdot \Big[\Big({{{\hat r}^{\prime\prime}}\over{{r^{\prime\prime}}^2}}\Big)\rho(\vec {r^{\prime}}) \Big] d\tau^{\prime}

\end{align}

위 식에서 단위벡터 {\hat r}^{\prime\prime}만 벡터이고 나머지는 모두 스칼라에요. 그리고 물리적 의미 도출을 위해 ({{{\hat r}^{\prime \prime}} / {{r^{\prime \prime}}^2}})를 한데 묶었어요.

한편 \psi를 스칼라함수, \vec A를 벡터장이라고 할 때 곱셈규칙(product rule) \nabla \cdot (\psi \vec A) = (\nabla \psi)\cdot \vec A + \psi \nabla \cdot \vec A를 적용하면 아래와 같아요.

\tag{2-5}
\begin{align}
\nabla \cdot \vec E &= {1 \over {4 \pi \epsilon_0}} \int \Big[\nabla \rho(\vec {r^{\prime}}) \cdot\Big({{{\hat r }^{\prime \prime}}\over{{r^{\prime \prime}}^2}}\Big) \\[10pt] 

&~~~~~~~~~~~~~~~~~~~~~~~~+ \Big(\nabla \cdot {{{\hat r}^{\prime \prime}}\over{{r^{\prime \prime}}^2}}\Big) \rho (\vec {r^{\prime}})\Big]d \tau^{\prime}
\end{align}

이때 \rho는 상수이므로 기울기 \nabla \rho는 0이 됩니다. 결국 위 식은 아래와 같이 쓸 수 있어요.

\tag{2-6}
\begin{align}
\nabla \cdot \vec E &= {1 \over {4 \pi \epsilon_0}} \int  \color{red}\Big(\nabla \cdot {{{\hat r}^{\prime \prime}}\over{{r^{\prime \prime}}^2}}\Big)\color{black} \rho (\vec {r^{\prime}})d \tau^{\prime}
\end{align}

그런데 윗식의 빨강색 부분은 델타함수에서 설명드렸던 -(1/r)의 라플라시안과 같아요. 결국 빨강색 부분은 델타함수를 이용해 4 \pi \delta^3(\vec {r^{\prime \prime}})이 됩니다.

이를 반영하면 (2-6)식은 다음과 같아요.

\tag{2-7}
\begin{align}
\nabla \cdot \vec E &= {1 \over {4 \pi \epsilon_0}} \int  4 \pi \delta^3 (\vec {r^{\prime \prime}}) \rho(\vec {r^{\prime}})d\tau^{\prime}
\end{align}

또한 [그림 1]에 따르면 \vec {r^{\prime \prime}} = \vec r - \vec {r^{\prime}}이 성립하므로 다음과 같이 바꾸어 쓸 수 있어요.

\tag{2-8}
\begin{align}
\nabla \cdot \vec E &= {1 \over {4 \pi \epsilon_0}} \int  4 \pi \delta^3 ( \vec r - \vec {r^{\prime}}) \rho(\vec {r^{\prime}})d\tau^{\prime}
\end{align}

또한 델타함수는 우함수이므로 다음과 같이 쓸수도 있어요. 그리고 상수 4 \pi는 약분할께요.

\tag{2-9}
\begin{align}
\nabla \cdot \vec E &= {1 \over {4 \pi \epsilon_0}} \int  4 \pi \delta^3 ( -(\vec {r^{\prime}} - \vec {r})) \rho(\vec {r^{\prime}})d\tau^{\prime}\\[10pt]
&= {1 \over {\cancel{4 \pi} \epsilon_0}} \int  \cancel{4 \pi} \delta^3 (\vec {r^{\prime}} - \vec {r}) \rho(\vec {r^{\prime}})d\tau^{\prime}\\[10pt]
\end{align}

결국 3차원 델타함수의 성질에 따라 윗 식은 아래와 같이 표현할 수 있어요.

\tag{2-10}
\begin{align}
\nabla \cdot \vec E ={{ \rho (\vec r)} \over{\epsilon_0}}
\end{align}

여기서 중요한 것은 전하들이 분포한 \rho(\vec {r^{\prime}})이 아닌 임의로 정한 공간에서의 \rho(\vec{r})로 바뀌었다는 거에요. 즉 어느 부피 V안에 전하밀도가 있으면 전기장의 발산이 있고, 전하밀도가 없으면 전기장의 발산은 0이 됨을 뜻합니다.

마지막으로 위 (2-10)식의 양변을 부피적분하면 다음과 같이 (1-1)식의 가우스 법칙과 같아져 발산정리가 성립합니다.

\tag{2-11}
\int_V (\color{black}{\nabla \cdot \vec E} \color{black})d\tau = {1 \over \epsilon_0}\int_V \rho (\vec r) d \tau = {{Q_{enc}}\over{\epsilon_0}} = \oint_s \vec E \cdot d \vec a

3. 전기장의 발산 의미

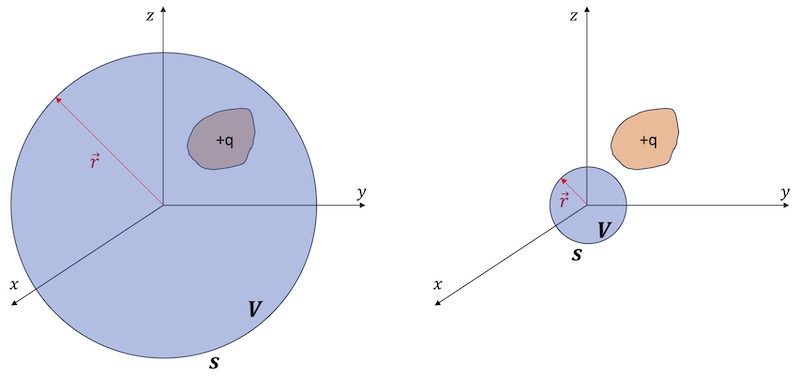
아래 [그림 2]에서 푸른색의 구가 가우스 곡면을 나타냅니다. 그 가우스 곡면 안쪽의 부피를 V, 그 표면적을 S라고 해봐요.

[가우스 곡면 안에 전하가 있는 경우]

그런데 왼쪽 그림의 경우에는 가우스 곡면 안에 알짜 전하 +q가 있는데요.

그림에는 그리지 않았지만 여러분들은 그 알짜전하로부터 전기장(또는 전기력선)이 나가는 방향으로 존재한다는 것을 상상해야 합니다. 화살표로 표현해봤더니 너무 복잡해져서 전기력선을 그리지 않았어요.

이 경우 가우스 표면 s를 통과하는 전기장선속은 아래와 같이 표현될거에요.

\tag{3-1}
\oint_s \vec E \cdot d \vec a = {{+q}\over{\epsilon_0}}

그렇다면 전기장의 발산은 어떻게 될까요? (2-10)식에 따라 다음과 같이 구할수 있어요.

\tag{3-2}
\nabla \cdot \vec E = {{\rho}\over{\epsilon_0}} = {{+q}\over{(4/3)\pi r^3 \epsilon_0}}

그럼 (3-2)식의 양변을 부피 V에 대해 적분해봐요. 그러면 다음과 같습니다.

\tag{3-3}
\begin{align}
\int_V (\nabla \cdot \vec E) d \tau &=  {{+q}\over{(4/3)\pi r^3 \epsilon_0}} \int_V d\tau\\[10pt]
&={{+q}\over{\cancel{(4/3)\pi r^3} \epsilon_0}} \cancel{(4/3)\pi r^3}\\[10pt]
&={{+q}\over{\epsilon_0}}
\end{align}

(3-1)식과 (3-3)식의 결과가 같은 것으로 보아 (2-11)식의 발산정리가 성립함을 알 수 있어요.

이와 같이 가우스 곡면안에 알짜전하가 있으면 전기장의 발산은 \rho / \epsilon_0가 됩니다.

[가우스 곡면 밖에 전하가 있는 경우]

이번에는 [그림 2]의 오른쪽 그림을 보세요. 이때는 가우스 곡면 밖에 전하가 있으므로 가우스 표면 s를 통과하는 전기장선속은 아래와 같이 표현될거에요.

\tag{3-4}
\oint_s \vec E \cdot d \vec a = {{0}\over{\epsilon_0}}=0

이번에는 전기장의 발산을 구하는데요. 이 경우에도 가우스 곡면안에 전하밀도가 있어야 하는데 전하가 없으므로 \rho가 0이 됩니다. 따라서 전기장의 발산은 0이 되요.

\tag{3-5}
\nabla \cdot \vec E = {{0}\over{\epsilon_0}} =0

그러므로 위식의 양변을 부피적분해도 0이 되죠.

\tag{3-6}
\int_V (\nabla \cdot \vec E)d \tau = 0

이 경우에도 (3-4)식과 (3-6)식은 같은 결과를 얻으므로 발산정리는 여전히 성립합니다.

가우스 곡면안에 알짜전하가 있으면 전기장의 발산이 \rho / \epsilon_0로 주어진다는 것을 알았어요. 이것은 가우스 곡면을 통과하는 전기장 선속이 0이 아니라는 의미이기도 해요. 아울러 이러한 성질은 전하가 홀로 독립적으로 존재하는 전기 홀극 성질을 갖기 때문에 가능해요. 즉 양전하와 음전하가 항상 함께 있는 것이 아니라 각각 독립적으로 존재할 수 있다는 의미죠.

만일 전기홀극이 아닌 양전하와 음전하가 항상 쌍(마치 자석의 N극과 S극이 항상 쌍으로 존재하는 것처럼)으로 존재한다면 가우스 곡면안의 알짜전하는 항상 0이 되므로 전기장의 발산도 항상 0이 되어야만 할거에요.

Related posts.

가우스 법칙 (Gauss’s law) 자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 자동차의 최고출력 개념과 이 값이 크면 무엇이 좋은가? 인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 밀도 정의와 활용 사례 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요.