Last Updated on 2024-03-03 by BallPen
SEM은 주사전자현미경(Scanning Electron Microscope)의 약자입니다. 이번 글은 SEM과 관련된 기초 물리학 이론에 대한 내용입니다.
SEM에 대한 다른 글들도 다양하게 보실 수 있습니다.
(1) 주사전자현미경과 관련된 기초 물리학 이론
(2) 주사전자현미경의 전체적인 구조와 구성
(3) SEM 전자총 원리와 총을 갖고 싶던 어린 시절의 값비싼 추억
(4) 주사전자현미경에서 ‘주사’란 무엇인가?
SEM 이론
SEM 이론 은 빛과 물질의 이중성에 대한 내용에서부터 출발합니다.
드브로이 물질파
광전효과와 콤프턴효과는 빛의 입자성에 대한 대표적인 증거입니다. 한편 빛의 간섭과 회절은 빛의 파동성에 대한 대표적 증거들이죠.
빛은 하나인데 어느 때는 입자이기도 하고 어느 때는 파동이기도 합니다.
신기한 것은 입자적 성질이 나타날 때는 파동적 성질은 사라지고, 파동적 성질이 나타날 때에는 입자적 성질은 사라집니다.
빛의 이러한 특성을 빛의 이중성이라고 합니다.
1924년 드브로이(Louis de Broglie)는 빛이 이중성을 갖듯이 다른 물질들도 파동과 입자의 이중성을 지녀야 한다고 주장하였습니다.

(출처: “From the October 1927 Fifth Solvay International Conference on Electrons and Photons” by iharsten is licensed under CC BY 2.0)
당시 이것은 매우 혁명적인 생각이었습니다. 얼마 후 1927년에 데이비슨과 저머(Davisson-Germer)는 비로서 결정으로부터 산란된 전자(입자)가 회절무늬(파동적 성질)를 형성한다는 사실을 실험적으로 규명하였습니다.
이로써 드브로이의 가설을 입증한 것이죠.
정지 질량이 없는 빛의 입자덩어리인 광자의 에너지와 운동량은 p=E/c의 관계가 성립합니다. 여기서 E는 광자의 에너지이고, c는 빛의 속력입니다.
또한 광자의 에너지는
\tag{1} E = h f = {{hc}\over{\lambda}}
로 주어집니다. 여기서 h는 플랑크상수, f는 진동수, \lambda는 파장입니다. 그러므로 광자의 운동량은
\tag{2} p = {{E}\over{c}} = {{hc}\over{c\lambda}} = {{h}\over{\lambda}}
으로 표현됩니다. 그러므로 질량이 m이고 속력이 v인 입자의 운동량은 mv=p이므로 입자가 갖는 파장은
\tag{3} \lambda = {{h}\over{p}} = {{h}\over{mv}}
로 주어지게 됩니다.
(3)식이 뜻하는 것은 질량을 갖는 입자가 움직이게 되면 파동이 형성된다는 중요한 의미를 갖습니다.
광학현미경
작은 물체를 확대하기 위해 예전부터 우리 인류는 유리 렌즈를 사용한 광학현미경을 활용해왔습니다.

(출처: “Opening of the ZEISS Forum and Museum of Optics” by ZEISS Microscopy is licensed under CC BY 2.0)
광학현미경은 전자기파 스펙트럼 대역 중 가시광선 영역의 빛을 이용하여 확대된 물체의 상을 만들어 냅니다. 이때 가시광선 영역의 빛을 이용하는 이유는 사람 눈에 보이는 유일한 전자기파 대역이기 때문이죠.
가시광선은 400 nm부터 700 nm의 파장을 갖습니다. 그런데 이 가시광선을 이용하여 광학현미경을 만들면 지극히 작은 물체는 관찰할 수 없습니다. 그 이유는 빛의 회절 때문에 분리된 두 물체가 마치 붙은 것처럼 보이는 현상이 나타나기 때문이죠.
분리된 두 점을 구분할 수 있는 최소의 크기를 분해능이라 합니다. 광학현미경의 분해능은 사용되는 빛의 파장의 절반 정도로서 이상적인 경우 200 nm (약 머리카락 굵기의 1/500 정도) 정도입니다.
따라서 200 nm보다 작은 물체는 광학현미경을 아무리 잘 만들어도 관찰할 수 없게 됩니다.
가속된 전자가 만드는 짧은 파장
이와 같이 광학현미경이 갖는 200 nm 정도의 분해능 한계는 사용되는 빛의 파장이 가시광선 영역이기 때문입니다.
만일 현미경에서 사용되는 빛의 파장이 더 짧다면 분해능도 작아져 더 작은 물체를 관찰할 수 있게 됩니다. 물론 400 nm 보다 더 짧은 파장은 사람 눈에 더 이상 보이지 않기 때문에 적절한 검출기가 개발되어야 하는 것은 필연적입니다.
이러한 배경하에서 개발된 것이 주사전자현미경(SEM, Scanning Electron microscope)입니다.
주사전자현미경은 입자인 전자(electron)가 갖는 파동적 성질을 이용합니다. 아주 빠르게 움직이는 전자가 만드는 파장이 어느 정도인지 아래의 예제를 보시기 바랍니다.
(문제) 1.00 \times 10^7~\mathrm{m/s}의 속력으로 날아가는 전자의 드브로이 파장을 구하여라.
(풀이) 전자에 대한 값들을 (3)식에 대입하여 파장을 구합니다.
\begin{align*}
\lambda &= {{h}\over{mv}} = {{6.63 \times 10^{-34}~{\mathrm{J \cdot s}}}\over {(9.11 \times10^{-31} ~\mathrm{kg} ) (1.00 \times 10^7~\mathrm{m/s})} } \\[10pt]
&=7.28 \times 10^{-11}~\mathrm{m}
\end{align*}SEM의 개발
위 문제 풀이에서와 같이 빠르게 움직이는 전자의 물질파는 약 0.07 nm의 파장 값을 갖게 됩니다. 이 정도의 파장값은 X선 대역에 해당하죠.
따라서 광학현미경이 최대로 관찰가능한 200 nm 크기 보다 훨씬 작은 크기의 물체를 쉽게 관찰할 수 있습니다. 요즈음의 주사전자현미경은 최대 약 0.5 nm의 분해능을 갖는 제품도 있습니다.
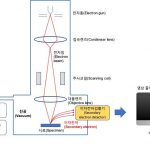
아래 이미지는 일반적인 주사전자현미경실의 모습을 보여주고 있습니다. 테이블 한 끝에 기계 장치가 보이는데 그것이 주사전자현미경 본체입니다. 사람들 앞 책상 위에 전자현미경을 컨트롤하는 장치가 있으며, 모니터에는 확대된 물체의 상이 디스플레이되는 모습입니다.

(출처: “d2540-6” by USDAgov is licensed under CC BY 2.0)
SEM 이론 관련 내용을 정리하면,
- 주사전자현미경은 아주 빨리 움직이는 전자(electron)가 갖는 드브로이 물질파를 활용한다. 대략적인 가장 짧은 파장 범위는 X선 정도이다.
- 그러므로 광학현미경으로 관찰할 수 있는 최대 분해능인 200 nm 보다 작은 물체를 주사전자현미경으로 관찰할 수 있다.
- 최신의 주사전자현미경은 분해능이 최대 0.5 nm 정도이고, 투과전자현미경은 0.1 nm 정도로 원자도 관찰 가능하다.






3 thoughts on “SEM 이론 – (1) 주사전자현미경과 관련된 기초 물리학 이론”